|
It is very useful to formulate problems using
vector notation and relations when
that is possible. Some of the problems illustrate that fact.
In setting up 1.10, 1.17, and LD1, write the relevant velocities as
vectors, then combine, and apply the constraints. Recall that velocities
add vectorially. You should be thoroughly familiar with velocities
written in spherical and cylindrical coordinates, that is, in terms
of the orthogonal unit vectors
 , 
 ,
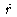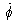or , ,
 .
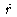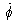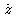Remember that the unit vectors in these coordinate frames
change upon differentiation. Other coordinate systems may appear later.
|
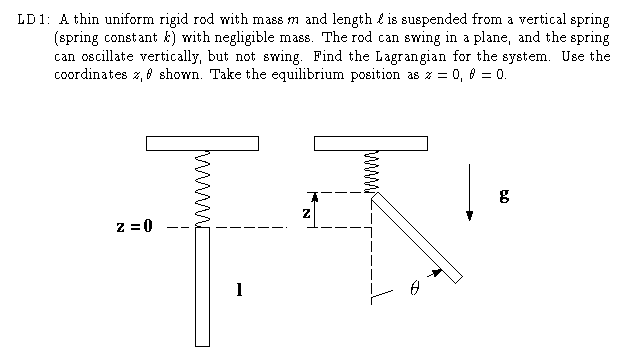
| 1.10: It is rather easy to set the problem up using
vector notation for the
velocities of the two masses in terms of their relative velocity and the
velocity of the central point on the rod. (How does the constraint of fixed
length of the rod come in? You may have built it in without thinking about
it explicitly!) Don't use Cartesian coordinates in this problem!
1.13: The force is an attraction toward the center. Be sure you get the full Lagrangian, with the correct sign for U. 1.17: Be careful taking the derivatives! |
