8.13(b): Transform the Lagrangian to the rotating system,
then find H. The results of LD12 will be useful.
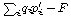 .
.
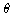 and t, and "orbit" integrals
for
and t, and "orbit" integrals
for 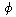 and
and 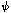 .
.
PROBLEM SET 10
Due Wednesday, November 25, 1998
Reading: Goldstein, Chap. 8 (skip pp. 358-361), Secs. 9.1-9.4
Problems: Goldstein, 8.13, 8.19, 8.22 (skip the last line), 8.32 (first part only); LD 18
|
8.13(a): Recall that p is the
canonical momentum, not the kinetic momentum.
The Hamiltonian must
be expressed as a function of p and r.
Use vector notation in (a) instead of breaking the expressions into
rectangular components - vector notation is more compact and also reveals
the structure and subtleties in the problem.
8.13(b): Transform the Lagrangian to the rotating system,
then find H. The results of LD12 will be useful.
| ||
| 8.19: Write the new Lagrangian as L' = L + dF/dt where F is a function of the q's and t only. Show that Hamilton's equations stated in terms of p', q', H' are equivalent, though not identical, to the original equations of motion in terms of p, q, H. Note that H' is a function of p', q', not p, q, and that derivatives with respect to one of the variables are calculated with the conjugate variable fixed. | ||
This problem shows that we can change
the canonical momenta and the Hamiltonian without changing
the form of Hamilton's
equations of motion. The transformation is a canonical transformation with
a generating function 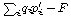 . .
|
||
8.22: The Hamiltonian is rather simple when written
in terms of the canonical mometa and Euler angles, though this seems rather
unlikely at the outset. To reduce the problem to quadratures, i.e., to
the evaluations of integrals, use the constants of the motion to derive
the relation between 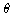 and t, and "orbit" integrals
for and t, and "orbit" integrals
for 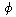 and and 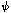 . .
|
||
| 8.32: Use a variational argument based on Hamilton's principle in the Hamiton-Weiss form, and introduce Lagrange multipliers to handle the differential form of the constraints. Recall Goldstein Sec. 2.4. |

LD18: Use the Hamiltonian from Prob. 8.22. Start by finding
the conditions under which a steady precession is possible. A sketch of the
effective potential in 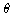 will help.
Call its second
derivative at the minimum B. It is not possible to solve explicitly for the
angle will help.
Call its second
derivative at the minimum B. It is not possible to solve explicitly for the
angle 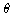 at which the steady precession
occurs, but
you can determine the defining condition and use the resulting relation
to make some simplifications elsewhere. at which the steady precession
occurs, but
you can determine the defining condition and use the resulting relation
to make some simplifications elsewhere.
|
||
| Why do we not consider perturbations in the constant momenta? What would changes in these quantities do, if anything? |
Send comments or questions to: ldurand@hep.wisc.edu
© 1997, 1998, Loyal Durand