 |
|
It is useful in problems involving changes of the coordinates q to start
with the Lagrangian rather than the Hamiltonian formulation of the problem, change variables there, and then determine the new canonical momenta and
Hamiltonian. That is the procedure followed here, with the new Lagrangian
given. The alternative in a purely Hamiltonian description is
to construct the generating function F(q,P) for the point transformation of
the coordinates and use that to determine the new momenta, and then transform
the original Hamiltonian.
|
| |
Parabolic coordinates are used to separate and solve the Schrödinger
equation for the Coulomb scattering problem in quantum mechanics. The
separation allows one to find analytic expressions for the quantum version of
the Rutherford scattering amplitude and cross section. (See, for example,
L. Schiff, Quantum Mechanics, Sec. 21 and the end of Sec. 16.
Note, however, that Schiff uses a different definition of the parabolic
coordinates with 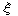 2, 2,
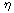 2 replaced by 2 replaced by
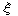 , , 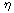 .) In contrast,
separation in spherical coodinates only gives the scattering amplitude as an
infinite partial-wave series, not a very useful result. .) In contrast,
separation in spherical coodinates only gives the scattering amplitude as an
infinite partial-wave series, not a very useful result.
|
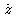 the vertical.
For the last question, it is useful to note that
the vertical.
For the last question, it is useful to note that
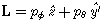 where we choose standard spherical
coordinates with
where we choose standard spherical
coordinates with 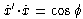 . The question is
why
. The question is
why 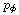 = Lz and
= Lz and
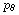 =Ly'
have a vanishing bracket while Lz and Ly do not.
What is different about Ly and Ly' or
=Ly'
have a vanishing bracket while Lz and Ly do not.
What is different about Ly and Ly' or
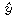 and
and 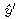 ?
?

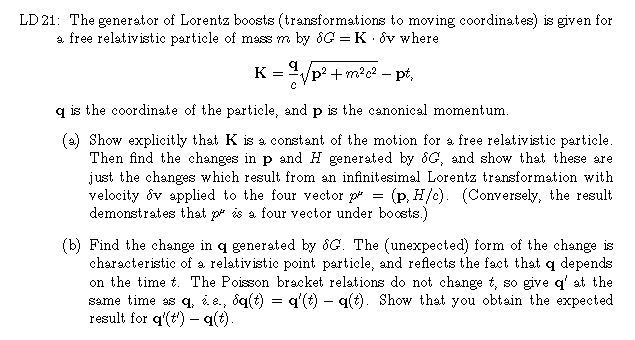

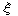 2,
2,
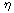 2 replaced by
2 replaced by
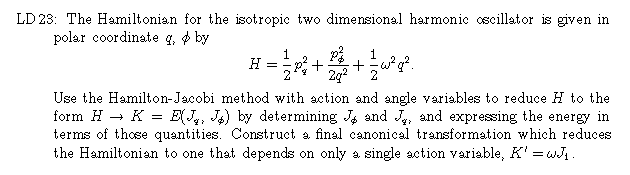
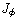 . The integral for
. The integral for 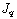 can be evaluated by writing it as an integral
between the turning points (the points qmin and qmax
where dWq/dq vanishes) and using q2 as the integration
variable. See Goldstein Eqs. 10-108c and 10-116 for an
alternative evaluation of the resulting radial integral.
can be evaluated by writing it as an integral
between the turning points (the points qmin and qmax
where dWq/dq vanishes) and using q2 as the integration
variable. See Goldstein Eqs. 10-108c and 10-116 for an
alternative evaluation of the resulting radial integral.