| 2.2 is more
difficult than most if tackled in general. The general solution is not
expected, but is worth studying. It can be described in terms of
the intersection of a sphere with a plane through the center of the
sphere provided you choose the integration constants properly (and remember
your analytic geometry from advanced calculus!)
|
||
| To get an easy solution, use
spherical coordinates with the initial point on the polar axes. This choice
is always possible - why?
|
||
|
2.3: Don't forget the constants of integration in the solution.
How are they to be determined? And don't assume from the beginning
that the motion takes place on a cycloid - that is what is to be shown!
|
||
| Motion on a cycloid has the interesting property that it is isochronous: the length of time which it takes for a particle to slide to the bottom starting at rest is independent of the height at which it is released. You may wish to show this. The time is a minimum only for the conditions which give the brachistochrone. There are various interesting applications of this result. |
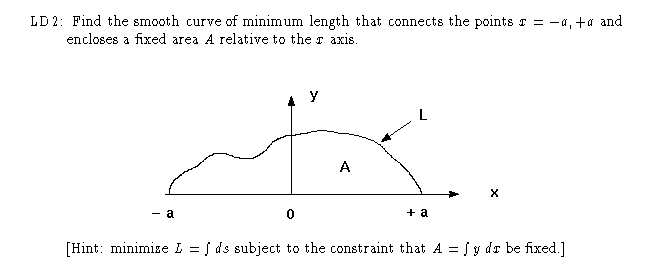

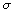 .
The algebra here can get messy so think before you calculate!
Part (a) illustrates the appearance of an unexpected Lagrangian constraint
through the Euler-Lagrange equations, and the elimination of this
holonomic constraint by elimination of one variable.
.
The algebra here can get messy so think before you calculate!
Part (a) illustrates the appearance of an unexpected Lagrangian constraint
through the Euler-Lagrange equations, and the elimination of this
holonomic constraint by elimination of one variable.
 and
and