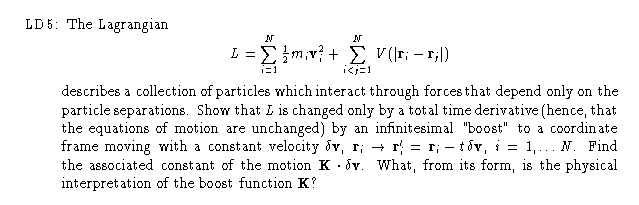Comments and hints:

2.11: Use polar coordinates with the angle measured from the top of the hoop to describe the motion. Suppose that the particle has a nonzero angular velocity initially, and find the general solution for the angle at which it leaves the hoop. Conservation of energy will be useful in the solution.

2.17: It is easy to see the instability by expanding the Hamiltonian in powers of the angular displacement of the particle, assumed small, from the bottom of the hoop. Explain why. But get the general condition for the stable point.

This problem gives an example of a bifurcation of solutions, dynamical symmetry breaking, or of a dynamical phase or state transition in which an initially stable "vacuum" (the lowest energy state of the system) becomes unstable and replaced by a new stable vacuum state. The original solution remains as an unstable equilibrium. The words used in this description indicate some of the other places in which phenomena of this type are important.

Comment:

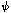New concept: The Schrödinger wave function is an example of a field, a continuous function of a spatial coordinate x (and the time in general). is the dynamical generalized coordinate. x is not a dynamical variable, but simply specifies where the field is measured, just as t in q(t) specifies when the dynamical coordinate q is measured. H is the Hamiltonian density for the field.

The (real) integral E is just the expectation value of the ordinary Schrödinger Hamiltonian p²/2m + V(x) for the given wave function . The result of this problem shows that the solution to the Schrödinger equation minimizes the energy E. This is the basis for the Rayleigh-Ritz variational method for estimating energies of quantum mechanical systems.

Question and comment:

This is a problem on the use of Noether's theorem. The boost operator K has a simple physical interpretation. What is it? And why, knowing its interpretation, should K be a constant of the motion?

The operations corresponding to boosts to moving coordinate frames, translations and rotations of the coordinates, and translations in time all give constants of the motion for isotropic translation invariant systems with time independent forces. The operations are those of the "Galilei group", the group of transformations of Galilean relativity. These are replaced for relativistic systems by the operations of the Poincaré group which we will see later.

Comment:

The isotropic oscillator has a large group of symmetry transformations, the group SU(n) of n-dimensional unitary transformations. We are establishing only a subset here. The rest will appear when we go to the Hamiltonian form of mechanics.

 

Send comments or questions to: ldurand@hep.wisc.edu

FURTHER OPTIONS:

© 1997, 1998, Loyal Durand