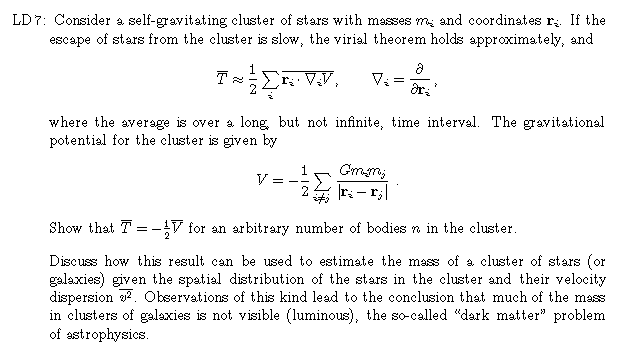3.14: Use the orbit integral approach to solve this problem.
Determine r explicitly as a function of 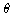 using the initial condition that r is at the inner turning point and
using the initial condition that r is at the inner turning point and
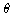 = 0 at t = 0.
The ``precession of the ellipse'' means that the orbit is
approximately an ellipse, but doesn't quite close: the angle at which
r returns to its minimum value
changes with each radial oscillation by some amount = 0 at t = 0.
The ``precession of the ellipse'' means that the orbit is
approximately an ellipse, but doesn't quite close: the angle at which
r returns to its minimum value
changes with each radial oscillation by some amount
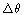 , which is to be determined. , which is to be determined.
|
| 3.23a Be careful deriving the equations of motion!
The crossed E and B fields of the magnetic
monople and electric charge lead to an E×B flow of
momentum around the symmetry axis of the system, hence to an angular momentum
directed along the axis. The system will therefore act like a gyroscope, a
fact apparently first noted by J.J. Thomson.
|
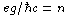 ,
n = 0, 1, 2, ..., i.e., the possible charges e are integer multiples of a basic
unit if there is even a single monopole in the universe. Alternatively, given
e, the condition determines the very large monopole charge. A quantum
mechanical argument first given by Dirac shows that n should properly be
replaced by ½n, the "Dirac quantization condition".
,
n = 0, 1, 2, ..., i.e., the possible charges e are integer multiples of a basic
unit if there is even a single monopole in the universe. Alternatively, given
e, the condition determines the very large monopole charge. A quantum
mechanical argument first given by Dirac shows that n should properly be
replaced by ½n, the "Dirac quantization condition".
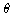 = 0
at that point.
= 0
at that point.