Hint:
Start by finding the Lagrangian of the system in the limit of small angles.
The upper and lower masses are m1 and m2,
respectively. Call the
characteristic angular frequencies 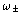 .
The actual construction of the solution for the given initial conditions
can be messy. It will help to express the elementary solutions in terms
of the trigonometric functions .
The actual construction of the solution for the given initial conditions
can be messy. It will help to express the elementary solutions in terms
of the trigonometric functions 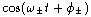 . .
|


