| 4.9 is a typical "rolling without slipping" problem. What is the instantaneous motion, and how is it connected to rotation and the constraints in the problem? (Think of Euler's theorem.) Vector methods are useful in setting up the problem. |
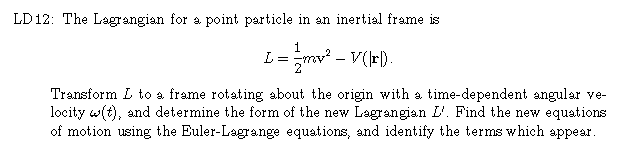
| This approach to the problem of transforming to rotating coordinates is simpler than the standard approach of transforming the equations of motion, and is useful in more general settings. |

LD13(a): You can specify the axis of rotation in
terms of 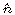 , the vector of direction cosines, but
should be sure to normalize it
to unit length. The somewhat unexpected form of the results for , the vector of direction cosines, but
should be sure to normalize it
to unit length. The somewhat unexpected form of the results for
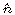 and and 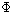 , with the
appearance of trigonometric functions of half angles, is characteristic
of the SU(2) representation. The half angles disappear in the actual
rotation of a vector represented by the matrix X = , with the
appearance of trigonometric functions of half angles, is characteristic
of the SU(2) representation. The half angles disappear in the actual
rotation of a vector represented by the matrix X = 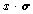 . .
|
||
| ||
LD13(b): The relations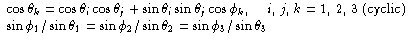 from spherical geometry will be useful. The angles  i are the sides of a
triangle on the unit sphere. The angles i are the sides of a
triangle on the unit sphere. The angles  i
are the opposite interior angles of the triangle. The use of the
abbreviated notation Ci = cos i
are the opposite interior angles of the triangle. The use of the
abbreviated notation Ci = cos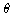 i, ci = cos(
i, ci = cos(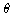 i/2),
Si = sin i/2),
Si = sin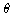 i,
si = sin( i,
si = sin(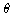 i/2)
will make it easier to manipulate the intermediate expressions you get. i/2)
will make it easier to manipulate the intermediate expressions you get.
|
||
| ||
You will find that
a coordinate system carried through a sequence of rotations that
returns the z axis to its original orientation
is generally subject to an extra rotation that
does not show up for a vector along z which is carried through
the same set of rotations. The vector simply returns to itself. The
difference is shown by the inequality of the
rotation angles and unit vectors 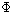 , ,
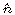 and and
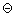 , , 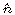 ' obtained
in (a) and (b). The extra
rotation is through the "spherical excess" angle ' obtained
in (a) and (b). The extra
rotation is through the "spherical excess" angle
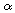 , the angle by which
the sum of the interior angles of the spherical triangle traced by the
three rotations exceeds
180°. This is just the area of the triangle on the unit sphere. Explain
in terms of the transformation of the matrix V = , the angle by which
the sum of the interior angles of the spherical triangle traced by the
three rotations exceeds
180°. This is just the area of the triangle on the unit sphere. Explain
in terms of the transformation of the matrix V = 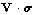 why a
vector V along the z axis is unaffected by the rotations above. why a
vector V along the z axis is unaffected by the rotations above.
|