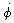5.16: See the figure below for the definition of the coordinates. Find the equations of motion and describe the motion qualitatively, with a sketch, for the initial conditions v = 0 and . You do not need to obtain an analytic solution. [Hint: use Lagrange multipliers to remove the constraints.]

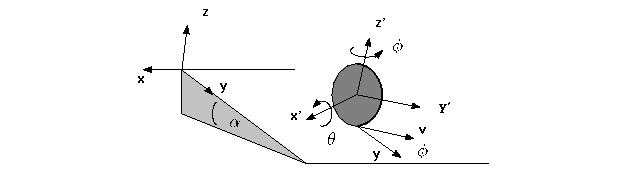
Comment: It is not difficult to solve the problem. You might want to try an analytic solution for the initial conditions given to see if the result agrees with your qualitative conclusions. What is the path?

Solve in terms of trigonometric or hyperbolic functions as appropriate. Relate the solutions using Euler's equations, and sketch the possible orbits carefully giving the directions of motion in the various regions, clearly labelled. As remarked in the problem, the pattern you will get is characteristic of small motions near stable and unstable equilibria.

Send comments or questions to: ldurand@hep.wisc.edu

FURTHER OPTIONS:

© 1997, 1998, Loyal Durand