 |
|
LD17(a) is a straightforward relativity problem, but is important
in providing the connection between Newtonian gravity and general relativity.
The mass m is included to make that connection
in a familiar form. However, m is an overall factor
in S, so drops out of the equations of motion. This disappearance of m
is a consequence, at a deeper level, of Einstein's principle of equivalence.
The result for the line element does not distinguish between massless and
massive particles, so the equations for geodesic motion can be used for either
kind of particle.
|
| | |
 |
|
LD17(b) combines ideas from throughout the course - geodesic
motion, the orbit equation, turning points, and scattering -
in the context of relativity.
The methods needed are not new, but are simply used in a new setting.
Recall the treatment of the
scattering angle in Goldstein, Sec. 3.10, use the constants of the
motion to obtain an expression for 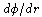 ,
and integrate to obtain the scattering angle. It is better to leave the
orbit integral in terms of r, with the physical situation clear,
than to make Goldstein's substitution u = 1/r. Your result for
the deflection should justify the first-order treatment in GM/c2. ,
and integrate to obtain the scattering angle. It is better to leave the
orbit integral in terms of r, with the physical situation clear,
than to make Goldstein's substitution u = 1/r. Your result for
the deflection should justify the first-order treatment in GM/c2.
|
| | |
 |
|
The deflection of light passing the sun is one of the classic predictions
and tests of general relativity. The use of starlight, as in the historic
observations by Eddington during the solar eclipse of 1919, has been
replaced by the deflection of signals from astronomical
radio sources and the related measurement of the gravitational time delay
in radar signals passing near the sun. The deflection and time delay
are now very accurately measured, and agree with
the theory. The gravitational deflection of light also leads to imaging
of distant galaxies by foreground galaxies as predicted by Einstein. This
"gravitational lensing" is a hot topic now.
|
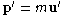 in rectangular coordinates
using the ordinary time. Use the results to find
in rectangular coordinates
using the ordinary time. Use the results to find
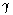 (known in terms of p and m) and
(known in terms of p and m) and
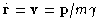 . Do the general problem with a
nonzero initial momentum perpendicular to the electric field.
. Do the general problem with a
nonzero initial momentum perpendicular to the electric field.
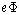 , and L = T - V. Use polar coordinates in the
plane perpendicular to the angular momentum L (why is it conserved?), and integrate the orbit equation to relate the angle to the radius.
The result from Prob. 3.14 will be useful: just identify the constants that
appear here with those in 3.14 when the orbit equations are written
in the same form. A rederivation of the final analytic result for the
rate of precession is not needed, but work out the new number.
, and L = T - V. Use polar coordinates in the
plane perpendicular to the angular momentum L (why is it conserved?), and integrate the orbit equation to relate the angle to the radius.
The result from Prob. 3.14 will be useful: just identify the constants that
appear here with those in 3.14 when the orbit equations are written
in the same form. A rederivation of the final analytic result for the
rate of precession is not needed, but work out the new number.
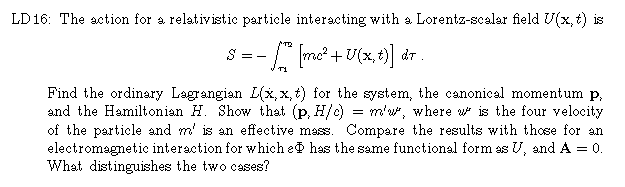
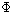 of electromagnetic theory is actually the timelike component of the 4 vector
A = ( A,
of electromagnetic theory is actually the timelike component of the 4 vector
A = ( A, 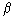 or
or 

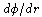 ,
and integrate to obtain the scattering angle. It is better to leave the
orbit integral in terms of r, with the physical situation clear,
than to make Goldstein's substitution u = 1/r. Your result for
the deflection should justify the first-order treatment in GM/c2.
,
and integrate to obtain the scattering angle. It is better to leave the
orbit integral in terms of r, with the physical situation clear,
than to make Goldstein's substitution u = 1/r. Your result for
the deflection should justify the first-order treatment in GM/c2.