C. N. Yang on statistical mechanics:
C. N. Yang made part of his early reputation in statistical mechanics,
calculating,
for example, the magnetization in the two-dimensional Ising model of a
ferromagnet. He subsequently worked on particle physics, inventing modern
gauge field theory ("Yang-Mills theory"), and winning the 1957 Nobel Prize
for his formulation with T. D. Lee of tests for parity violation in weak
interactions. Yang and Lee also did considerable work together on
statistical and solid state problems. Yang's influence and the techniques
he introduced still persist, e.g., in the "Yang-Baxter" equations which
appear in many problems and were first introduced by Yang (Phys. Rev. Letters
19, 1312 (1967)).
The following is the written version of a
short talk Yang gave on some historical
developments in statistical mechanics in the twentieth century. It is well
worth reading to get an overall picture of some of the principal developments
as seen by a master of the subject (and of many other subjects), and for his
commentary on some of the leading theorists of the era.
Remarks About Some Developments in Statistical Mechanics
Chen Ning Yang
SUNY-Stony Brook and the Chinese University of Hong Kong
(Talk given at the Xiamen Conference, July 31-August 4, 1995)
Gibbs and Equilibrium Statistical Mechanics
In 1901, at the age of 62, Gibbs (1839-1903) published a book called
Elementary Principles in Statistical Mechanics (Dover, New York). It was
remarkable in several ways. First, it had as a subtitle
The Rational Foundation of Thermodynamics. Gibbs chose this subtitle
because he knew his theory did not agree with experiments, as he emphasized in
the preface to the book. Yet he believed there were no other possible rational
basis to thermodynamics. Second, the style of writing of the book has an
elegance akin to a long poem, which is quite unique in the history of physics.
Third, it was to become the fundamental basis of twentieth century equilibrium
statistical mechanics.
A year before Einstein's death in 1955, he was asked who were the most powerful
thinkers he had known. He replied (Ref. 1), ``Lorentz'', and added, ``I never
met Willard Gibbs; perhaps, had I done so, I might have placed him beside
Lorentz''.
Origin of Bose-Einstein and Fermi-Dirac Statistics
In the last chapter of Gibbs' book mentioned above, he found it necessary to
insert a factor N! in the formula for the free energy:
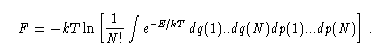 This factor made F an extensive quantity. Furthermore it was convenient for
treating mixtures of atoms. Later on the factor h^N was inserted in the
denominator to make the quantity under the logarithm dimensionless. But the
factor N! remained mysterious and was called the problem of the ``absolute
entropy constant''. It was believed to be related to the fact that for
identical
particles, the phase space should not be multiply counted, but the precise
meaning of this factor, especially for small N, was not clarified.
This factor made F an extensive quantity. Furthermore it was convenient for
treating mixtures of atoms. Later on the factor h^N was inserted in the
denominator to make the quantity under the logarithm dimensionless. But the
factor N! remained mysterious and was called the problem of the ``absolute
entropy constant''. It was believed to be related to the fact that for
identical
particles, the phase space should not be multiply counted, but the precise
meaning of this factor, especially for small N, was not clarified.
In June 1924 Bose's paper was published. He derived Planck's radiation law by
counting states of photons in a novel way. As soon as Einstein saw this paper,
he generalized it to the counting of states of atoms, thereby predicting the
phenomena of Bose-Einstein condensation, a most daring and insightful
extrapolation which has only now been brilliantly experimentally confirmed.
A year and a half after Bose's and Einstein's papers, upon reading Pauli's
article on the exclusion principle, Fermi realized in 1926 that he had now the
concepts in hand to discuss the thermodynamics of a collection of electrons.
The results were such fundamental concepts like the Fermi sea, the Fermi
energy, etc.. According to Rasetti (Ref. 2), Fermi was not influenced by the
earlier work of Bose and of Einstein.
Also in 1926, Heisenberg pointed out that the difference between the singlet
and triplet energy levels of the (1s)(2s) states of He was due to the
difference of the symmetry of the space wave function, which in turn was caused
by the requirement of antisymmetrization of the total wave function of the two
spinning electrons.
Finally in August 1926 Dirac developed the general theory of the symmetry of
wave functions of Bose-Einstein and Fermi-Dirac particles.
Incidentally this chain of papers Einstein-Fermi-Heisenberg-Dirac reveals in a
dramatic way the differences of styles of these four great physicists:
-
Einstein's prediction of Bose-Einstein condensation of free particles was
against all intuitive concepts of phase transitions at that time. To make such
a prediction, without full mathematical rigor, based on a novel counting method
extrapolated from photons to atoms, required a perception and a boldness that
was uniquely Einstein's.
-
Fermi's paper formed the basis of all subsequent
theories about condensed matter physics. It has the hallmark of Fermi's
physics: the ability to capture the fundamentals of the problem at hand and
extract from it the essence that will affect all future developments. Solidity
and imagination marched hand-in-hand in Fermi's work.
-
Heisenberg's work
produced the key idea that on the one hand linked the symmetry of wave
functions to Pauli's exclusion principles and on the other hand resolved the
great puzzle of how the spin alignment of two electrons can affect the Coulomb
energy of the He atom. Furthermore the idea of the ``exchange integral'' which
originated in this paper later produced another great achievement of
Heisenberg's: the mechanism of ferromagnetism. However, Heisenberg's paper was
long on originality but short on elegance and precision, a characteristic of
all of Heisenberg's papers.
-
In contrast, Dirac's papers were always elegant
and precise. They also tend to be the final word in the problems that they
address. In the case of his 1926 paper, very little can be added later to his
masterly analysis.
Early Discussions of Phase Transitions in Statistical Mechanics
The development of quantum mechanics in 1925-1927 removed the difficulties that
Gibbs had to face in checking his rational foundation against experimental
facts. Thus was born quantum statistical mechanics. In the late 1920's and
early 1930's, physicists and chemists applied the new quantum statistical
mechanics to many problems in dilute gases and dilute solutions with great
success.
Then in the mid 1930's, because of the discovery of peaks in the C(p)
versus T
curve in alloys, the theory of order-disorder transformations became quite
fashionable. An ``order parameter'' was introduced for the discussion of phase
transitions. Such theories are now called mean field theories, which actually
was first used by Weiss (Ref. 3) in 1907 for describing ferromagnetic
transitions.
In 1937 J. Mayer attempted to formulate a theory of liquid-gas transition
without introducing mean fields by examining the convergence properties of the
virial series. There was a ``vigorous discussion'' of his ideas at the Van der
Waals Centenary Congress (Ref. 4) on November 26, 1937 in Amsterdam, followed
in the next months by elaborations/alternations of Mayer's theory.
Incidentally, my own entry into statistical mechanics was related in a way to
Mayer's theory. I was an undergraduate student in Kunming in 1941-1942 when
Professor J.S. Wang gave several lectures on this theory of Mayer's and on
subsequent developments. I did not then quite understand the complexities of
the theories, but became fascinated with the subject (Ref. 5). That led to my
working with Wang for my Master degree thesis on statistical mechanics. As to
Mayer's theory, some ten years later in two papers (Ref. 6) Lee and I cleared
up the confusion in this field.
Onsager and the ``Ising Disease''
In 1944, in an amazing paper, Onsager solved the two dimensional Ising model
rigorously. It was the first in a field which undoubtedly will be covered in
many presentations at this Conference. His paper was very difficult to read
because he did not describe his strategy. He seemed to have a predilection for
calculating the commutators of every other expression in sight without telling
what he was aiming at. I still remember vividly today how I was frustrated in
trying to understand that paper, first when I was a graduate student in China
and then a graduate student in Chicago. It was many years later, in March 1965,
that I finally learned (Ref. 7) how it had come about that Onsager was so fond
of calculating those commutators.
Young physicists today may find it surprising, even unbelievable, that in the
1950's the Ising model and similar problems were not deemed important by most
physicists. They were considered arcane exercises, narrowly interesting,
mathematically seducing, but of little real consequence. There was the phrase
(Ref. 8), for example, of ``contracting the Ising disease''.
In a recent article
by Dyson in my Festschrift (edited by S.T. Yau, published by the International
Press) he recalled how, in 1952, when he read my article about the
magnetization of the Ising model, he was impressed by the beautiful complexity
of the calculation and the beautiful simplicity of the result, but felt I was
wasting my time.
The situation dramatically changed around 1960 because of several
developments:(1) the experimental discoveries (Ref. 9) of divergences of
specific heats near various phase transition points; (2) theoretical work on
the critical exponents led gradually to the concept of universality and to some
very useful inequalities among the critical exponents; and (3) the proposal of
a scaling law (Ref. 10).
With all these developments equilibrium statistical mechanics finally became
respectable and was considered physically important in the 1960's.
-
A. Pais, Subtle is the Lord, the Scientific Biography of
Albert Einstein, (1982).
-
R. Rasetti in Collected Papers of Enrico Fermi, vol. 1, p. 178 (University
of Chicago Press, 1965).
-
P. Weiss, J. of Physics 6, 667 (1907).
-
M. Born and K. Fuchs, Proc. Roy. Soc. A166 , 391 (1938).
-
Chen Ning Yang, Int. J. Mod. Phys. B2 , 1325 (1988).
-
C. N. Yang and T.D. Lee, Phys. Rev. 87 , 404 (1952); T.D. Lee and
C. N. Yang, Phys. Rev. 87 , 410 (1952).
-
Chen Ning Yang, Selected Papers 1945-1980 with Commentary, p. 11-13
(Freeman, 1983).
-
A. Pais, Nucl. Phys. 5 , 297 (1958).
-
W.M. Fairbank, M.J. Buckingham and C.F. Kellers, Proceedings of the Fifth
International Conference on Low Temperature Physics (Madison, Wisconsin)
p. 50.
See also W.M. Fairbank and C.F. Kellers in Critical Phenomena, National
Bureau of Standards Miscellaneous Publication 273 (1965); W.K. Robinson and
S.A. Friedberg, Physical Review 117 , 402 (1960); M.I. Bagatskii,
A.V. Voronel
and V.G. Gusak, J. Exp. Theor. Phys. (in Russian),
43 , 728 (1962). [English translation: Soviet Physics JETP 16 ,
517.]
-
B. Widom, J. Chem. Phys. 12C , 3898 (1965).
Send comments or questions to:
ldurand@theory2.physics.wisc.edu