Advice: Before starting the problems, look at the homework information to see what I expect in solutions, and for advice on working together. Note, in particular, that you are expected to provide detailed explanations of your calculations and interpretations of your results.

		Hint: In part (b), think about the final configuration of the system ignoring surface effects. It is neither necessary nor especially useful to try to describe microscopically how the system got there. This concentration on the final configuration is typical for problems in equilibrium statistical mechanics as contrasted, for example, to problems in kinetic theory
		Comments: LD1 is a typical counting problem in condensed matter physics. The connection with thermodynamics and the behavior of vacancies in real solids comes in through the use of Boltzmann's definition of the entropy in terms of the statistical weight, and the observation that each vacancy costs a finite excitation energy quantum mechanically. Note that 1/T is initially just an abbreviation for a particular derivative of S. The connection with the usual temperature can be established by showing that T is the same for two systems in equilibrium, and that it can be connected to a measureable property such as the pressure in a gas thermometer. We will demonstrate these properties later. The temperature of the solid could then be measured using a gas thermometer in equilibrium with it. Why is the result you get not given by a simple Boltzmann factor?

Comments: LD2 illustrates several properties of large systems. Note the following, in particular: (a) The statistical weights are very large. Even 10 is a large number. It is therefore useful to use logarithms and Stirling's approximation for the gamma function or factorial, and treat the weight as continuous even for numerical work. The weight is very sharply peaked about its maximum value for N large. (b) It is sufficient here (but not in the numerical calculatons in (a)) to use the truncated form of Stirling's approximation, x! = x ln x - x + .... Why are two situations different? (c) can be treated as a numerical problem. The Boltzmann entropy S is an extensive quantity proportional to N up to negligible non-extensive corrections of order ln N. The two different definitions of the entropy also give the same result up to logarithmic corrections. If you want to see analytically what is going on, expand ln to second order in its Taylor series in n0 around the peak. This gives a Gaussian approximation for which can be used to evaluate the total statistical weight as an integral. The result stated follows when you observe that n+, n0, n- and all scale linearly with N for E/N fixed. We will introduce further definitions of S later. The equivalence of the different definitions depends on the statistical weights being sharply peaked. (d) The relative weights with which the numbers of particles in different substates appear are given by the expected ratios of Boltzmann factors once T is introduced. This result, which is not at all obvious in the original statement of the problem, is again generic for large systems.

Comments: Note the units! We will generally use Gaussian cgs units in dealing with microscopic problems. They do not contain the annoying factors and 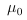needed to get to SI units, and the speed of light c appears explicitly as needed for relativistic problems. In part (b), H is the energy or Hamiltonian of a single spin. This problem deals with Pauli's theory of spin paramagnetism, a quantum phenomenon, as a simple counting problem using the Boltzmann definition of the entropy. The natural parameter for describing statistical systems is the inverse temperature 1/T as we will see later in discussing Gibbs' approach to statistical mechanics. This parameter can vary from plus infinity (T --> 0+) to minus infinity (T --> 0-), and goes smoothly through zero at infinite T, with an accompanying change in the sign of T. It is therefore sometimes said rather colorfully that negative temperatures are "hotter" than infinite temperatures. Negative temperatures can actually be produced in isolated systems that remain out of equilibrium with their surroundings for a long time. See the references given.

FURTHER OPTIONS: