

PROBLEM SET 12
Due Friday, May 5, 2006
Reading: Landau and Lifshitz, Secs. 148-150, 152-153
Huang, Secs. 14.1-14.4, 16.1-16.4


| Comment:
"This year's homework is next (?) year's Nobel Prize"? Could be! (Written in 1996 - Cornell, Ketterle, and Wieman actually received the prize for their work on Bose-Einstein condensation in 2001.)
This is a problem of continuing interest for current work. The first direct observation of the Bose-Einstein condensation was a striking result of a set of tour de force experiments at nanoKelvin temperatures. Our homework examples have now covered statistical phenomena with T from 10-9 K to 10+7 K, a span of sixteen decades.
The method used to calculate the integral in (a) can be used with
a further common scaling of the values of p' and r' along each of the principal
axes to evaluate the integral in the case of the anisotropic oscillator. The
result for Tc is changed by the replacement of the angular
frequency omega of
the isotropic oscillator by the product of the principal frequencies raised
to the 1/3 power.
|
||
| In the course of evaluating the the number distribution for temperatures such
that N0/N = 0, 0.1, 0.3, 1.0 with r/r0
in the range given, you should see a central peak containing the
condensate emerge. A reasonable lower limit in a semilogarithmic
plot of the radial
number density is around 0.0001: the excited state contribution to the density
is very small for r/r0 small. It is also illuminating to plot the
normalized radial number distribution 4pi (r/r0)2
dN/Nd(r/r0) which shows
more clearly the radii at which the bulk of the particles are located.
The very rapid change in the shape of the number distribution with T is quite striking, and shows up clearly in the experimental results. A useful test of the numerical results in (b) is given by the condition that the total distribution in the form given must integrate numerically to 1. That is, all the atoms are someplace in the radial distribution. How does dN(r) vary with r for r -> 0 and T < Tc? You can determine this using the identity used to determine the chemical potential of the ideal Bose gas for T -> Tc+. |

| Comment:
This is a classic problem. The same formal result for the magnetization
was obtained by Weiss before the advent of quantum mechanics, but the
interaction parameter which appeared had an unphysically large value when
interpreted in terms of the interaction between atomic magnetic moments.
The discrepancy was explained by Heisenberg who showed that the interaction
was actually electric rather than magnetic, but depended on the spins
through the Pauli exclusion principle.
|
||
| The model reappeared as a mean field approximation for the Ising model. It is being used here to show in what sense the Landau approach to phase transitions approximates the correct results. The range of validity of the expansion of the free energy in powers of m will be clear whan the exact and approximate results for the magnetization and the magnetic susceptibility are compared in (b). |

| Comment:
The model in this problem contains the essence of first-order transitions
such as the liquid-gas transition in a van der Waals gas. The van der Waals model can be interpreted as a kind of mean field
model in which the effects of particle interactions are included in an
average sense through the excluded-volume and pair-interaction corrections
to the equation of state for the ideal gas.
Expansion of the van der Waals equation near the critical
point (T = Tc, P = Pc, V = Vc) gives an expression of the form above with coefficients which
depend explicitly on t = T/Tc as shown in Landau and Lifshitz,
G = (p - 4t)v + 3tv2 +3v4/8, p = P/Pc, v = V/Vc.
The transitions near the critical point can be studied in detail as
in the present problem.
|
||
The mean field behavior of the van der Waals gas near Tc was
actually derived
and used in Prob. LD15 (b) and (c) on critical
opalescence. The isothermal compressibility 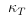 (isothermal response) was
found there to diverge as 1/t for t -> 0 corresponding to a critical exponent (isothermal response) was
found there to diverge as 1/t for t -> 0 corresponding to a critical exponent
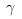 = 1. = 1.
|

| Comment: This is a typical Landau free energy problem. The important points are to find out how to use the conditions for the minimization of F, first for h identically zero, and then for general h but fixed t, and to get acquainted with the various critical exponents. |