Comments: The problem illustrates the use of Gibbs' method for determining a statistical distribution using known average quantities, but assuming that there are no other constraints on the system (an assumption of maximum ignorance about unobserved quantities).
		The work of Chou, Yang, and Yen builds on a model introduced by Feynman. Feynman assumed that the rapidity distributions of particles produced in the "central region" in high-energy collisions were not sensitive to the constraints imposed by energy conservation, and would be flat, corresponding to a simple radiative d³p/E distribution in momentum, again with the transverse momenta limited. This is roughly correct, but the actual distributions fall off at large rapidities where the particles have a large fraction of the initial energy in the collision, and energy conservation becomes important. (Rapidity and pseudorapidity are equivalent for particles with E >> m, where m is the particle mass.) CYY go beyond Feynman, and include energy conservation in an average sense, though not event-by-event. The results obtained by CYY give a remarkably good description of the overall pseudorapidity distributions observed in high energy collisions, but fail to give the observed rapidity-dependent correlation between the particle multiplicity and the transverse momentum associated with the production of QCD jets.

		Comment: This problem deals with statistical calculations using the partition function, and with the use of a perturbation expansion to treat the effect of a small perturbation on an otherwise solvable problem. It is characteristic of approximation methods that they deal with expansions of extensive quantities, here the free energy F = -kTln Z, rather than with Z itself. We will see this systematically later.
		In (b), you will need to express Z1 as the product of the single particle partition function Z1(0) for no perturbation and a series in 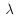, and then evaluate the coefficients in the series. To obtain the perturbed Helmholtz free energy F, relate Z to Z1 and expand the logarithm of Z1 to second order in .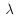

		Comment and hints: This problem involves an important application of the two-particle Boltzmann distribution to the calculation of the reaction rate that controls the luminosity of the sun. The integral which appears could be done numerically, but that approach would give little insight into the temperature dependence of the reaction rate. The approximate analytic calculation to be done here gives this insight, and is quite accurate.
		It is all right in this calculation to ignore the variation over the peak of the multiplicative factor p left from the integration weight d3p, and to work only with the exponential terms, but you can correct for the extra factor without difficulty. This method for approximating sharply peaked integrals is frequently useful. Finally, before trying to get a numerical value of T6 at the end, think about which of the factors in the analytic expression varies most rapidly with T, and concentrate on that. It will be useful to take a logarithm; the problem is then easily solved numerically by iteration starting with the dominant term in T.

FURTHER OPTIONS: