
PROBLEM SET 7
Due Friday, March 24, 2006
Reading: Landau and Lifshitz, Secs. 33, 45-52

| This problem illustrates the difficulty one has in trying to treat problems with Fermi or Bose statistics directly. Part (a) shows that the quantum partition function ZN factors for distinguishable particles just as it did classically. Factorization is lost in part (b), and it is clear that the construction of ZN for N large will be much more difficult for identical particles with the constraints from Fermi or Bose statistics taken into account. |

Hint: Use the series expansion of eA, find the
structure of a general term  assuming that A and
assuming that A and 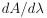 do not commute, and
then use trace identities to rearrange the results. do not commute, and
then use trace identities to rearrange the results.
It is very useful in a variety of problems to be able to express
averages of dynamical quantities in terms of derivatives of an appropriate
partition function. The construction here shows how this works for first
derivatives even when A and  . .
|

| Comment:
This problem involves a calculation of
quantum paramagnetism and a direct investigation of the "classical" limit.
This limit can be derived a different way. In particular,
the quantum description of paramagnetism involves a sum over
magnetic quantum numbers. The sum can be replaced approximately by an
integral for J sufficiently large, with m/J regarded as
the cosine of the angle between J and the magnetic field
as in the "vector model" for angular momentum. This reproduces the
classical expression for Z seen for electric dipoles in LD13, and
integration gives the classical result for the partition function.
The approximation of the sum by an integral becomes legitimate in
just the circumstances
you will need when approximating the exact quantum result directly as
suggested in the problem.
Note that the elementary moments depend explicitly on Planck's constant h. This makes it appear that the magnetization should vanish in the classical limit h --> 0. However, one does not really need the strict classical limit h --> 0 to get Langevin's result. What condition does one need? |

| Comment:
It is usually argued in elementary treatments of rotating molecules
that diatomic molecules cannot rotate about the axis joining the atoms.
If so, rotation contributes only kT rather than 3kT/2
to the energy of the molecule, and the total specific heat per molecule is
the observed C=5k/2 rather than 3k. This result violates
the classical equipartition theorem, which gives a rotational energy
3kT/2 for any values of the principal moments of inertia.
The rotation of a diatomic molecule can be treated essentially exactly in quantum mechanics. It is therefore possible to investigate how the classical result appears as a limit of the quantum mechanical result, and in particular, why rotation around the body axis is not excited at normal temperatures. That is the goal of the problem. |