Comment: The direct series expression for the rotational partition function Z cannot be summed exactly. The series converges very rapidly at low temperatures, and no summation is necessary. However, many terms contribute to the sum at high temperatures, and it is useful to have an approximate analytic expression for the result. High temperatures correspond to high excitation of the rotational energy levels, hence to Bohr's correspondence limit, and one would expect to find the classical partition function for the rotator as the leading term in an expansion in powers of 1/T. The presence of a large number of significant terms in the series suggests that it could be useful to approximate the sum by an integral. The integral gives the classical result, as will be seen. The Euler-Maclaurin formula gives a systematic way of relating the sum to the integral, hence of calculating the corrections to the classical result. The resulting expression is known as Mulholland's formula. The Euler-Maclaurin summation formula is useful in a number of problems of this type.

Comment: The symmetry conditions imposed by Fermi and Bose statistics have remarkable effects on the temperature dependence of the rotational specific heats of homonuclear diatomic molecules. The calculation here shows that Mulholland's formula gives a good approximation for the rotational partition function when the series in even and odd values of the orbital angular momentum l appear with equal weights. The effect of the Fermi statistics in this problem is to change the relative weights of the even and odd series, and to introduce large excursions in the rotational specific heat at low temperatures. Be careful with your numerical calculations! And try to figure out why crot behaves as it does.

		Comment: Be sure to give your expression for 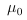in part (a). A key point is that the configuration integral may depend on the total number of molecules containing any of the isotopoes I, but does not depend on the division of this number among the individual isotopes. The result generalizes easily with the inclusion of molecules that do not involve the isotopes I. The construction in part (b) gives the kinetic theory definition of equilibrium. In (c) construct a careful argument to establish what is to be expected as temperatures change. It is useful to consider a simple model and analyze what should happen to the character of the precipitation from a mass of temperate air as it moves toward colder regions, raining or snowing sporadically, and the long-term effect of this on the 18O/16O ratio in the atmosphere and ocean.
		Some applications:The use of the 18O/16O ratio in tracking temperature changes involves the comparison of measured ratios to the ratio in a standard sample deposited under known conditions. The results are usually given as (18O/16O) =(18O/16O)measured)/(18O/16O)reference - 1 in parts per thousand. See the results from Greenland ice cores: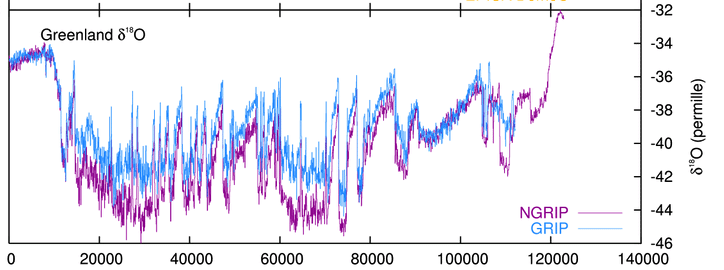 Longer records exist from Antartic ice cores giving a temperature history for some 750,000 years: (note: (18O/16O) is given in parts in 104) with an inferred temperature history 18O/16O analysis has been used recently to determine the time of uplift of Andean Altiplano [Science 311, 478,511 (2006)] and the Tibetan plateau [Science 311, 758 (2006)], and to trace monsoon precipitation for the past 160,000 years using calcite from stalagmites in the Dongge cave in China. So the results of this problem are useful in current geophysical research!

FURTHER OPTIONS: