Bipolar Junction Transistors

Murray Thompson

Sept. 5, 1999

---

1  Introduction

These notes follow those on pn junctions, in which the basic components of npn transistors were discussed.

2  A Reassurance

At this point, some students, who prefer to have precise calculations and exact theory, may start to become concerned about these sloppy methods, bad approximations and imprecise calculations. We can reassure them. In spite of these rough methods, the general concept of negative feedback (to be introduced later) will allow us to use these imperfect circuits yet gain extremely linear
circuits, extremely precise amplifications and precision measurements of our input signals.

First we must consider these imperfect amplifiers. The later feedback and precision circuits would be useless without them!

3  Summary of Bipolar Transistor ``theory'' so far

  1. The fraction of the electrons leaving the emitter and going to the collector instead of the base is normally called [(Icollector)/( Iemitter)] = a.

    More strictly, in case of non-linear behaviour, we define

    a = [(dIcollector)/( dIemitter)]

  2. The ratio of the collector current to the base current is normally called b. Thus, b = [(Icollector)/( Ibase)] From this we can get

    b = [(a)/( 1-a)].

    More strictly, in case of non-linear behaviour, we define

    a = [(dIcollector)/( dIemitter)]

  3. Hence (1-a)b = a

    a = [(b)/( 1+b)]

  4. By arranging the geometry so that the base region is very thin, most of the electrons entering from the emitter into the base will be fall over the edge down the steep electric potential fall of the base-collector junction before they meet and recombine with holes in the base.

    Thus, by making the base be very thin so that the emitter-base junction and the collector-base junction are very close, and doping the collector-base junction so that it is very thin (with a high electric field [E\vec] = -[dV/ dx], the fraction a of the electrons leaving the emitter and going to the collector instead of the base can be made close to 1.0 and

    b = [(a)/( 1-a)] can be made large. This can make the transistor more useful.

    While a transistor with a large b, such as b = 100, can be used to make amplifiers with a high gain, the thin base and collector-base junction have a general defect. This defect is that the thin collector-base junction will have high electric fields [E\vec] and avalanche breakdown may occur.

  5. So long as the collector-base voltage is greater than about 2 or 3 volts, very few of the electrons which fall over the collector-base junction can bounce back.

    Thus, So long as the collector-base voltage is greater than about 2 or 3 volts, the fraction a of electrons passing through both junctions is only slightly dependent upon the collector-base voltage.

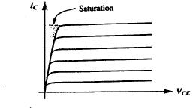
    A typical set of Icollector and VCollector-Emitter curves for equispaced base currents are shown below.

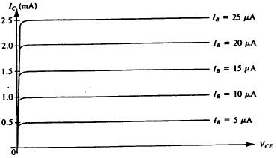
    pnp_11.gif
    Although the following curves are not usually shown in specifications, the following shows ICollector and IBase curves for equispaced collector voltages.

    pnp_22.gif

  6. Thus a and particularly b are useful parameters because they are nearly constant for any given bipolar junction transistor over a range of working voltages and currents.

    The b may vary from one transistor to another due to manufacturing variations and due to changing temperature. Note that IC in the following graph has a logarithmic horizontal scale and covers a very wide rage.

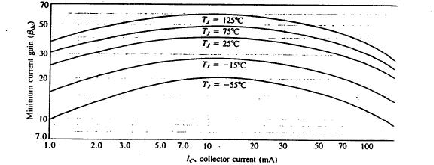
    pnp_33.gif
    Even though b does not change much with voltage and current, in any given transistor, the variation in b due to temperature and manufacturing is significant. The variation due to manufacturing, can be minimized by selecting transistors with particular values of b.

  7. In most practical circuits, we try to make the action be independent of b.

    This can be done in a variety of ways but will require that b be large so that b >> 1 and we can approximate functions like b+1 as b.

  8. The transistor is said to be in saturation if the collector voltage is too low.

    pnp_44.gif

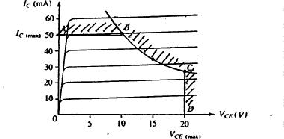
  9. Any transistor has maximum ratings for

    1. The maximum power giving a maximum product of IC max and VCE max.

    2. A maximum current into the collector IC max through its connecting wire and weld.

    3. A maximum voltage on the collector-base junction VCE max above which the junction may break down.

    pnp_55.gif

4  Transistor Model

By inspecting the transistor ICollector, VCE and b curves above, we can make a model of the actions within a transistor. Like some other models, the reproduction is imperfect but will allow us to make systems where the action is nearly independent of b.

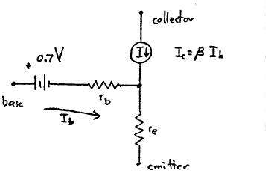
We want a 3-terminal model which we can use to ``replace the transistor'' when want to make calculations. In this model we assume

  1. The base-emitter junction is kept forward biased (``turned on'') by a small but sufficient base-emitter current to keep the base emitter voltage near 0.7 volt.

  2. The Base-Collector voltage is sufficient for the transistor to have a b > 10

A common convention is to use lower case r for each of the internal resistances to distinguish them from the normal external resistors we attach to the emitter, base and collector.

We will call the join of the 3 lines as the point ``join''.

We replace the base to emitter junction with a small 0.7 volt battery with a small (perhaps negligible resistor rb.

The current through the base is called Ib.

From the previous discussion of p,n junctions, we know that the emitter has the dynamic junction impedance (which may also be negligible) of about
re = 2 ohm + [0.026 volt/( Ibase)].

pnp_66.gif
We insert a ``Current Generator'' in the collector to cause a current IC = bIb.

5  Various Simple Amplifiers

We will now consider four general circuits corresponding to the 3 permutations of 1 terminal being ``shared'' between the circuitry of the input and output attached circuitry - the permutation of the common emitter is used twice. Each amplifier amplifies an input DC voltage which may change. By using an additional ``coupling capacitor'', each can amplify only the AC component of the input voltage.
  1. Grounded Emitter Amplifier

    The simple transistor model suggests how an amplifier might be made. We call this a grounded emitter amplifier.

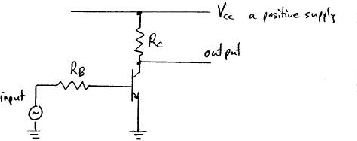
    pnp_77.gif
    Variations DVinput in the base input voltage will cause variations in the emitter current through rb. The transistor can be replaced for calculation purposes by the transistor model as in the next diagram. If, as usual, re is small, then

    DIb = [(DVinput)/( RB+rb)]

    and these will cause variations in the collector current

    DIc = bDIb = b [(DVinput)/( RB+rb)]

    The changing collector current flows through the collector resistor Rc from a constant voltage usually called ``Vcc'' and so the changing collector current causes the collector voltage to change by

    DVC = - RC b [(DVinput)/( RB+rb)]

    DVC = -([( RC b )/( RB+rb)]).DVinput

    Thus a small change in the input to the base can cause a larger change in the voltage of the collector.

    1. The ``voltage gain'' or ``amplification'' [(Vc)/( Vb)] = -([( RC b )/( RB+rb)]) is negative meaning that the output signal is inverted relative to the input signal. This is not an disadvantage but is actually an advantage for negative feedback and for digital circuitry.
    2. This circuit is very easy to understand but is seldom used for the following reasons.
    3. It is hard to make transistors with a particular precise value of b.

    4. In any transistor, b depends upon temperature
    5. b also depends, slightly, upon the collector voltage and collector current Ic. (In other words, the transistor model is not very precise.)
    6. rb depends, a little, upon temperature, Ib and Ic.
    7. re depends, a little, upon temperature, Ib and Ic.
    8. The voltage difference across the junction (near 0.7 volt) is temperature dependent.

    In general, the grounded emitter gives a high amplification but the voltage gain [(Vc)/( Vb)] is too unpredictable for this circuit to be used except in digital circuits.

    The following three amplifying circuits include some type of ``negative feedback'' to overcome these problems. Other circuits use transistors in identical pairs and use them to amplify pairs of voltages (one the signal and the other a constant voltage or a negative signal) so that some of the unwanted effects can cancel.

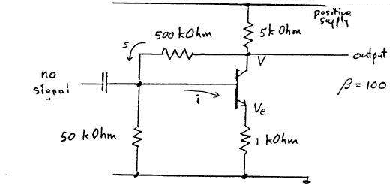
  2. Common Emitter Amplifier

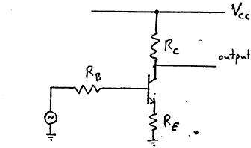
    pnp_88.gif
    This has 3 resistors as shown RB, RE and RC attached to the base, emitter and collector. The top ``rail'' is attached to a positive power supply (perhaps +10 Volt). The lower ``rail'' is the ground.

    The input is on the left (via the resistor RB. The output is on the right from the collector pin attached to the resistor RC.

    Apply a small incremental voltage DVin to the resistor RB leading to the base.

    The transistor can be replaced for calculation purposes by the transistor model as in the next diagram.

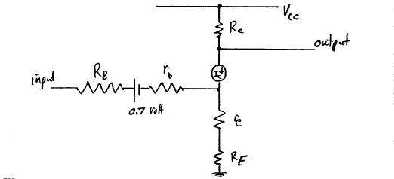
    pnp_99.gif
    We concern ourselves only with the current and voltage increments so can ignore the +0.7 volt battery. Define the voltage on the point below the current generator at the join of the 3 lines as DVjoin We can obtain 2 equations.

    1. The current increment DIBase into the base due to the voltage increment DVin is

      DIBase = [(DVin-DVjoin)/( RB+rb)]

    2. The current increment DICollector into the Collector due to the voltage increment DVin is

      DICollector = bDIBase

      The voltage increment across the actual resistor RE and the internal resistance re totalling RE+re, due to the two currents caused by the voltage increment DVin is

      DVjoin = (1+b)DIBase(RE+re)

    From these two equations

    DIBase = [(DVin- (1+b)DIBase(RE+re))/( RB+rb)]

    (RB+rb)DIBase = DVin- (1+b)DIBase(RE+re)

    (RB+rb)DIBase + (1+b)DIBase(RE+re) = DVin

    (RB+rb + (1+b)(RE+re))DIBase = DVin

    DIBase = [( DVin)/( (RB+rb + (1+b)(RE+re)))]

    From this, we can calculate 3 important parameters for this circuit.

    1. The Voltage Gain of the common emitter circuit
      The collector voltage will decrement due to the increased current through the resistor RC from the positive +10 Volt supply. Thus the voltage increment on the collector will be negative;

      DVC = -DICRC

      DVC = -bDIBaseRC

      DVC = -b[(DVin)/( (RB+rb + (1+b)(RE+re)))]RC

      Thus the voltage gain of this common emitter circuit is

      AV = [(DVC)/( DVin)] = -[(bRC)/( (RB+rb + (1+b)(RE+re)))]

      If we neglect both rb and re, then

      AV » -[(b(RC))/( (RC + (1+b)RE))]

      again, if we assume that b >> 1, the voltage gain, AV, becomes

      AV » -[(RC)/( RE)]

      Notes.

      • The gain is negative meaning that the output voltage signal is inverted.

      • Using the concepts of feedback, we say that the resistor RE is providing negative feedback so that in the approximations of b being high and rb and re being low,
        the voltage gain AV is minus(the ratio of the collector and emitter resistances)

    2. The Input Impedance of the common emitter circuit

      The Input Impedance is the ratio

      Zin = [(DVin)/( DIBase)]

      Use DIBase from above

      Zin = (RB+rb + (1+b)(RE+re))

      Again, if we neglect rb and re and assume that b >> [(RB)/( RE)] then

      Zin = bRE

    3. The Output Impedance of the common emitter circuit

      Remembering that the impedance of a current generator is infinite, the output impedance of the circuit looking back into the circuit is only that of the resistor RC to the power supply which is a virtual ground. Thus we have

      Zout = RC

  3. Common Collector Amplifier (The ``Emitter Follower'')

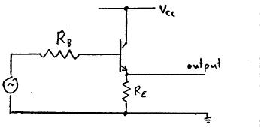
    pnp_100.gif
    This has 2 resistors as shown RB and RE attached to the base and emitter. The top ``rail'' is attached to a positive power supply (perhaps +10 Volt). The lower ``rail'' is the ground.

    The Collector is attached directly to the top rail at +10 Volt.

    The input is on the left (via the resistor RB. The output is on the right from the emitter pin attached to the resistor RE.

    Apply a small incremental voltage vin to the resistor RB leading to the base.

    The transistor can be replaced for calculation purposes by the transistor model.

    Apply a small incremental voltage DVin to the resistor RB leading to the base.

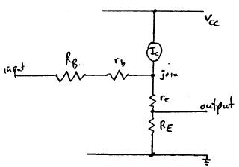
    pnp_111.gif
    We concern ourselves only with the current and voltage increments so can ignore the +0.7 volt battery. Define the voltage on the point below the current generator at the join of the 3 lines as DVjoin

    As with the Common Emitter before, we can obtain 2 equations.

    1. The current increment DIBase into the base due to the voltage increment DVin is

      DIBase = [(DVin-DVjoin)/( RB+rb)]

    2. The current increment DICollector into the Collector due to the voltage increment DVin is

      DICollector = bDIBase

      The voltage increment across the actual resistor RE and the internal resistance re totalling RE+re, due to the two currents caused by the voltage increment DVin is

      DVjoin = (1+b)DIBase(RE+re)

    From these two equations

    DIBase = [(DVin- (1+b)DIBaseRE)/( RB+rb)]

    (RB+rb)DIBase = DVin- (1+b)DIBase(RE+re)

    (RB+rb)DIBase + (1+b)DIBase(RE+re) = DVin

    (RB+rb + (1+b)(RE+re)DIBase = DVin

    DIBase = [( DVin)/( (RB+rb + (1+b)(RE+re)))]

    From this, we can calculate 3 important parameters for this circuit.

    1. The Voltage Gain of the common collector (emitter follower) circuit

      The current through the emitter is

      DIEmitter = (1+b)DIBase

      The voltage increment across RE is the output signal DVout

      DVout = DIEmitter RE

      DVout = (1+b)[( DVin)/( (RB+rb + (1+b)(RE+re)))] RE

      DVout = [((1+b)RE)/( (RB+rb + (1+b)(RE+re)))]DVin

      If we neglect re and rb

      DVout » [((1+b)RE)/( (RB + (1+b)RE))]DVin

      If b >> 1, then

      DVout » [((1+b)RE)/( (RB + (1+b)RE))]DVin

      The voltage Gain

      AV = [(DVout)/( DVin)] » [((1+b)RE)/( (RB + (1+b)(RE)))]

      If (RB << (1+b)RE then

      AV = 1.0

    2. The Input Impedance of the common collector (emitter follower) circuit

      The Input Impedance is the ratio

      Zin = [(DVin)/( DIBase)]

      Use DIBase from above

      Zin = (RB+rb + (1+b)(RE+re))

      Again, if we neglect rb and re and assume that b >> [(RB)/( RE)] then

      Zin = bRE

    3. The Output Impedance of the common collector (emitter follower) circuit

      To calculate this, we assume no change to Vin (ie DVin = 0) but draw a small current DIout from the output (emitter pin) and calculate or measure the resulting DVout.

      We concern ourselves only with the current and voltage increments so can ignore the +0.7 volt battery. Again, define the voltage on the point below the current generator at the join of the 3 lines as DVjoin

      As with the Common Emitter before, we can obtain 2 equations.

      1. DVjoin = -DIbase(RB+rb

      2. Vjoin = (b+1)DIbase re + ((1+b)DIbase-DIout)RE

      -DIbase(RB+rb = (b+1)DIbase re + ((1+b)DIbase-DIout)RE

      Grouping the Ibase terms on the right

      DIoutRE = DIbase[RB+rb+(1+b)(re+RE)]

      DIbase = [(DIoutRE)/( [RB+rb+(1+b)(re+RE)])]

      The change in the output voltage DVout is due to the two changes in current through RE

      DVout = ((increase in emitter current)-(current drawn from output))RE

      DVout = ((1+b)DIbase-DIout)RE

      DVout = ((1+b)[(DIoutRE)/( [RB+rb+(1+b)(re+RE)])] -DIout)RE

      The Output impedance is

      Zout = -[(DVout)/( DIout)] = -(1+b)[(RE2)/( [RB+rb+(1+b)(re+RE)])] +RE

      Zout = -(1+b)[(RE2)/( [RB+rb+(1+b)(re+RE)])] +RE

      Zout = -[((1+b)RE2)/( [RB+rb+(1+b)(re+RE)])] +RE

      Zout = [(-(1+b)RE2+[RB+rb+(1+b)(re+RE)]RE)/( [RB+rb+(1+b)(re+RE)])]

      Zout = [(+[RB+rb+(1+b)(re)]RE)/( [RB+rb+(1+b)(re+RE)])]

      If rb and re are very small

      Zout = [(RBRE)/( [RB+(1+b)RE])]

      If b is large

      Zout = [(RB)/( 1+b)]

      The output impedance has been lowered to a fraction [1/( 1+b)] of the RB. In this way, an emitter follower (common collector circuit) can be used to lower the effective output impedance of any device which might have had an output impedance of RE.

    The emitter follower (common collector) circuit is often used together with another circuit which might already provide sufficient voltage gain.

  4. Common Base

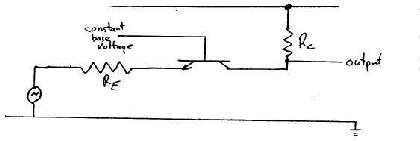
    pnp_122.gif
    This has 2 resistors as shown RE and RC attached to the emitter and collector. The top ``rail'' is attached to a positive power supply (perhaps +10 Volt). The lower ``rail'' is the ground.

    The Base is attached directly to a constant voltage, say +3.0 volt and so can act as a common reference point for both the input side and the output side.

    Define the voltage on the point below the current generator at the join of the 3 lines as DVjoin. Define the voltage on the point X below the current generator as DVX.

    The transistor can be replaced for calculation purposes by the transistor model as in the next diagram.

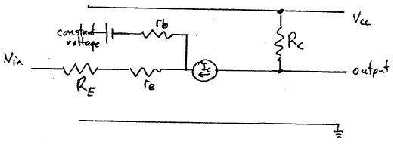
    pnp_133.gif
    We will later apply a small incremental voltage DIin to the point X between the resistor RE and the emitter.

    1. First, however, consider the circuit with no inputs signals (ie DIin = 0).

      The Transistor Model gives us the equivalent circuit for incremental voltages and currents.

      If Vb = +3.0 volt, then

      Vjoin = +3.0 volt-0.7 volt-rbIb
      		(1)

      The current through the resistor RE and internal resistance re is IC+Ib = (b+ 1)Ib

      The voltage at point ``join'' is

      Vjoin = (IC+Ib)(re+RE)

      Vjoin = (b+ 1)Ib(re+RE)
      		(2)

      VC = 10 volt -ICRC = 10 volt -(b+1)IbRC
      		(3)

      Use equations 1 and 2 to eliminate Vjoin.

      2.7 volt - rbIb = (b+ 1)Ib(re+RE)

      Ib = [2.7 volt/( rb+(b+1)(re+RE))]

      Substitute this Ib into equation 3.

      VC = 10 volt-(b+1) 2.7 volt
      rb+(b+1)(re+RE)
      		 RC
      		(4)

      --------

    2. Now calculate these again but with the addition of an input current Iin due to the signal introduced via a capacitor. Consider the circuit with an injected input current signal, DIin = 0.

      The Transistor Model gives us the equivalent circuit for incremental voltages and currents. Calculate the new values for Vjoin, IC, Ib, and VC.

      If Vb = +3.0 volt, then

      Vjoin = +3.0 volt-0.7 volt-rbIb
      		(5)

      The current through internal resistance re is IC+Ib = (b+ 1)Ib. However the current through the resistor RE will differ due to the input signal.

      The voltage at point ``join'' is

      Vjoin = (IC+Ib)re+(IC+Ib+DIin)RE

      Vjoin = ((b+1)Ib)re+((b+1)Ib+DIin)RE
      		(6)

      VC = 10 volt -ICRC = 10 volt -(b+1)IbRC
      		(7)

      Use equations 5 and 6 to eliminate Vjoin.

      2.7 volt - rbIb = ((b+1)Ib)re+((b+1)Ib+DIin)RE

      This can be simplified

      2.7 volt-DIinRE = (rb+(b+1)(re+RE))Ib

      Ib = [(2.7 volt-DIinRE)/( rb+(b+1)(re+RE))]

      Substitute this Ib into equation 7.

      VC = 10 volt-(b+1) 2.7 volt-DIinRE
      rb+(b+1)(re+RE)
      		 RC
      		(8)
      Compare this equation 8 with the previous equation 4. The injected input current DIin has changed the output voltage by

      DVout = New VC- Old VC = (b+1) DIinRE
      rb+(b+1)(re+RE)
      		 RC
      		(9)

      If re and rb are small,

      DVout » (b+1) DIinRE
      (b+1)(RE)
      		 RC
      		(10)

      DVout » DIinRC
      		(11)

      Note

      • a positive current injection through the input coupling capacitor causes a positive voltage excursion on the collector - NO INVERSION.

      • The output DVout is the same as if the injected current DIin were subtracted by the transistor from its current through the resistor RC to keep the current through RE constant. The current through the resistor RC changes by -DIin causing an output voltage excursion DVout » +DIinRC which has the same polarity as the input current signal.

    From this, as before we can calculate 3 important parameters for this circuit.

    1. The Voltage Gain of the common base circuit

    2. The Input Impedance of the common base circuit

    3. The Output Impedance of the common base circuit

6  A Useful form of the Common Emitter Amplifier

The common emitter amplifier needs the input voltage to be a few volts above ground so that, some current flows through the equivalent junction battery and some current flows through the collector to the emitter. We say we need to ``bias'' the base input to ensure the transistor stays in this working region where b is fairly constant. This is particularly important in the amplification of AC since the coupling capacitor blocks any DC input.

pnp_144.gif
A simple way of ``biassing'' the AC common emitter is to add two resistances with resistances higher than the emitter resistor so that the ``drain current'' draining down through both ``bias resistors'' satisfies two requirements.

  1. The drain current is much greater than the current into the transistor base so that the DC voltage at the base is determined by the bias resistors and the supply voltage rather than the transistor which is unpredictable and
  2. the two resistors, when seen from the input, do not present a low impedance. Since the amplifier may have been preceeded by a preamplifier, this requirement is usually that the input impedance of the two bias resistors should be large compared with the collector resistance of the preamplifier.

Often, these two conditions imply that the bias resistors must be kept between two limits which are a factor of about b apart. For example, if b is about b = 65, then choose bias resistors giving the following.

  1. A total bias drain current from supply to ground of about 8 times the transistor's base current and [8/ 65] times the emitter current.

  2. The parallel impedance of the two bias resistors about 8 times the output impedance of the previous amplifier.

7  A More Useful Form of the Common Emitter Amplifier

pnp_155.gif
The circuit is similar to the previous common emitter amplifier but the biasing structure has been changed to include some negative feedback from output signal on the collector. As a result, this circuit gives an amplification which is more predictable in spite of variations in the b of the transistor.

File translated from TEX by TTH, version 1.93.
On 6 Sep 1999, 18:33.