1  Purpose

• To construct a difference amplifier, to measure the DC quiescent point and to compare to calculated values.

• To measure the difference mode gain, the common mode gain, the common mode rejection ratio (CMRR) and to compare to calculated values.

• To understand the role of the common emitter resistor (R₁) in providing feedback necessary for differential operation.

• To explore examples of applications of difference amplifiers.

2  Discussion

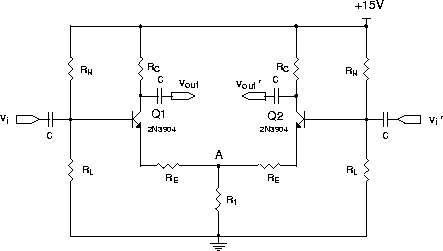
Read Horowitz & Hill (2nd Ed) page 98. That description is for a DC coupled difference amplifier using +15 volt and -15 Volt power supplies. Our amplifier is for AC signals, and uses only one power supply but we use the same notation.

If a linear amplifier has two receiving input voltages v_i and v_i^¢, then its output may be a linear combination of the two inputs:

v_out = X.v_i +Y.v_i^¢

where X and Y are two constants. We can manipulate this equation to give

v_out = [((X-Y))/ 2].(v_i-v_i^¢) +(X+Y).[((v_i+v_i^¢))/ 2].

In other words, v_out can be written as the linear combination of the difference (v_i-v_i^¢) and common mode or average [((v_i+v_i^¢))/ 2].

The difference amplifier provides a number of advantages which make it one of the most useful circuit configurations, particularly as an input stage for high gain and DC amplifiers. By choosing matched transistors, often on the same piece of silicon of an integrated circuit, very stable and drift free operation may be obtained because of the symmetry of the amplifier. The differential input is particularly useful in cases where the desired signal is the difference between the voltages on two wires, which might be masked by a large and varying voltage, with respect to ground, that is common to both wires. Operational amplifiers often consist of a cascaded series of difference amplifiers which provide excellent stability and high gain. An ideal difference amplifier has a large gain for difference mode signals (v_i = - v_i¢), and zero gain for common mode signals (v_i = v_i¢). We may write the output voltage (taken from either collector) for a real difference amplifier as:

If one uses only a difference mode signal (ie  v_c = 0), then A_d = v_°/v_d. For the common mode signal only (v_d = 0), the common mode gain can be measured A_c = v_o/v_c.

A figure of merit for real difference amplifiers is called the Common Mode Rejection Ratio, CMRR, which is defined as:

Figure 1: Schematic of the Difference Amplifier

For an ideal difference amplifier, CMRR would be infinite since A_c = 0, and for real amplifiers we want CMRR as large as possible. Consider the circuit shown in Figure 1. In the calculation sheet the gains and CMRR are derived and the results are:

[Sometimes, in technical books, this is carelessly given with inconsistent units as r_tr = @ 25/I_c(mA) + 2 ohm. Please do not use this notation.]

It is apparent that CMRR will become larger as R₁ becomes larger. The large R₁ acts as a current source and an active current source, using an additional transistor is often used when a very large CMRR is desired. The effect of R₁ may be understood by noting that, in the difference mode the currents in the two transistors are 180^° out of phase, resulting in zero net AC current through R₁, thus making point A an AC ground (a virtual ground). This means a large difference mode gain. In the common mode, however, twice the AC current flows through R₁ than through one transistor. In this case it appears that there is a resistor of value 2R₁ to ground and the common mode gain dramatically decreases. (For a true current source, the effective value of R₁ ®¥, giving A_c ~ 0.)

3  Procedure

This writeup contains a worksheet which will enable you to calculate the component values for the circuit. This must be done before the lab session.

1. Construct the circuit of Fig. 1. Check the lead assignments for the 2N3904 on the data sheets which you will find in the lab.
   1. Compare the measured values of V_b, V_c and V_e to those calculated in the handout.
   2. Is your circuit balanced (ie  V_c » V_c^¢)?
   3. Are both transistors turned on?
   4. Use trimming resistors in parallel with the calculated bias resistors as necessary in order to balance - The collector currents should be the same within » 30%.

2. Generate a source of common and difference mode signals. One way to do this is to use the supplied transformer. When the center tap is grounded, the signal at the end of the winding is balanced such that the voltage on one side is equal to, but 180^° out of phase with, that on the other. The difference input thus uses v_i from one side and v_i¢ from the other. The common-mode input uses both from the same side.

3. 1. Using these signals, measure A_d, A_c and the CMRR.
   2. Compare them to the calculated values.
   3. Note the relative phases of the signals at collectors of Q1 and Q2 and at point A.

4. The difference amplifier can be used with a one-sided input as a phase inverter.

   1. Feed an AC signal into the left input (v_i = AC signal) and ground the right input (v_i^¢ = 0) through the coupling capacitor.
   2. Examine the outputs v_out and v_out^¢ and the signal at point A.
   3. Explain why outputs v_out and v_out^¢ have opposite polarity.

5. If there is time, you might measure the bandwidth of the amplifier.

   1. Use a one-sided input v_i as in 4a above without the transformer. Put a 3.3 k resistor in series with the input.
   2. Measure the bandwidth.
   3. Now put a 250 pF capacitor across the collector to the base of Q.
   4. Remeasure the bandwidth.
   5. Then put a 1 mF capacitor across R_c, examine the output at the collector of Q^¢ and again remeasure the bandwidth.
   6. Discuss your observations.

4  Worksheet for the Difference Amplifier Laboratory

4.1  Calculation of the AC or Small Signal Gains

Refer to the difference amplifier circuit of Fig. 1. An AC equivalent circuit can be used to calculate the gains. To simplify the algebra we define R_f = r_tr+R_E. The gains and CMRR, which were derived before, can be rewritten:

Two current generators deliver currents i = bi_b and i^¢ = bi_b^¢ and we assume that b is large so that the base currents i_b and i_b^¢ can be neglected and the emitter currents can regarded as equal to the collector currents i_c and i_c^¢. Note that the inputs (the base connections) determine the voltages at the outer ends of the R_f resistors but do not supply an appreciable fraction of the current through them. (The base currents are only [1/( b)] of the collector currents.)

Figure 2:

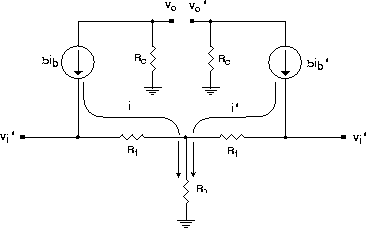
We can get 4 equations by applying ohm's law to this equivalent circuit.

A little algebra can be done on the 4 equations above to get them into the form
v_o = A_d(v_i-v_i^¢) + A_c(v_i+v_i^¢)/2. Start with equation 1 minus equation 2 :

Equation 3 minus equation 4 :

Substituting equation 6 :

Equation 1 plus equation 2 gives:

Equation 3 plus equation 4 gives:

Substituting equation 10 :

Adding equations 8 and 12 :

We can define v_d = (v_i-v^¢_i) as the ``Difference Mode'' input voltage and define v<sub>c</sub> = [((v<sub>i</sub>+v<sup>¢</sup><sub>i</sub>))/ 2] as the ``Common Mode'' input voltage.

Then equation 14 becomes

where

A_d = [(R_C)/( 2R_f)] is the ``Difference mode gain'' and A<sub>c</sub> = [(R<sub>C</sub>)/( 2R<sub>1</sub>+R<sub>f</sub>)] is the ``Common mode gain''.

5  Calculation of the Component values

We want to meet the 5 following goals for the desired operating characteristics of the amplifier. Here we have picked a set of parameters for the design.

1. We want to use a single supply voltage with a voltage of V_cc = +15 V

2. We want the Output impedance to be Z_out = 1k.

3. We want the Output Swing to be ±2 V.

   (We define the ``Output Swing'' as the maximum voltage excursion which can be generated on each of the outputs without the amplifier becoming non-linear. The Output Swing of 2 V means we would like the output v<sub>o</sub> to be able to change by ± 2 V and the output v<sub>o</sub><sup>¢</sup> to be able to change by ± 2 V with the outputs changing in opposite directions. Each output can change from its Q Point value by +2 V to -2 V, a difference of 4 V. We say that the ``peak to peak voltage'' is v_p-p = Dv_c = 4 V. Thus each transistor must be able to operate in linear mode while its collector changes over a total range of 4 V.)

4. The difference mode gain to be A_d @ 8.

5. We want the common mode gain A_c to be as low as possible, consistant with a common mode input range of ± 2.5 V. That is, the ± 2 V output swing should be available when the inputs are both 2.5 V higher or lower than the ``Q-point''. For example, if the two inputs are as shown, a difference amplifier will amplify the difference with a large gain and the average with small gain A_c.

   
   Figure 3:

• high difference mode gain,
• low common mode gain,
• good linearity,
• and possibly other features such as power used, cost and physical size

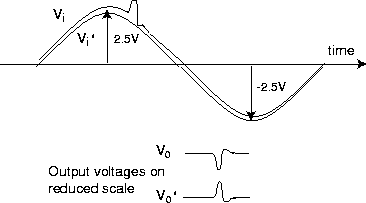
is called the ``Operating Point'' or ``Quiescent Point'' or ``Q Point''. The design choices to meet these goals are calculated below. You should follow this outline, make any necessary or suggested calculations and fill in the values in the next section.

1. First assume b is large to separate the tasks of

   1. first calculating the desired static voltages on the collectors, bases and emitters

   2. then, later in item , calculating the bias resistors R_H and R_L for each base

2. The output impedance assuming our Transistor Model (which assumes a current generator i.e. the impedance looking into the collector is high) is Z_out = R_C. To meet one of the goals, we choose R_C = 1 k.

3. Since R_C = 1 k and we want a 2 V output swing, we adopt the static current (ie average or DC current or quiescent) through each collector to be I_C = 2 mA. The collector current of each transistor can then swing 2 mA between 0 mA and 4 mA.

4. Since an increase from 2 mA in one transistor will occur only when a decrease from 2 mA occurs in the other transistor, the common resistor R₁ will carry a fairly constant 4 mA.

5. We can choose R_f to get the desired Difference Mode voltage Gain A_d = 8.

   1. A_d = R_C/2R_f and so R_f = [(R_C)/( 2A_d)].
      Since we want A_d @ 8,
      we have R_f @ [1.0 k/ 2×8] = 62.5 ohm.

   2. Since the base-emitter junction carries an average current of 2 mA,
      r_tr = (0.025 ohm-Amp/I_c + 2) ohm, and we have
      r_tr = ([0.026/ 0.002] + 2) ohm = 14.5 ohm.

   3. Since R_f = r_tr+R_E, R_E should be about (62.5 - 14.5) ohm » 47 ohm.

6. Use the following items to calculate R₁.

   1. We want the common mode gain A_c to be as low as possible consistent with other requirements:

      Ac = - RC 2R1 + Rf .

      Therefore we would like to make R₁ as large as practical. However, we must be careful to ensure the transistor remains in a linear mode and, for this, has v_c > v_tr+0.5 volt.

   2. The output swing of +2 V requires V_C = 13 V at the Q point. From the symmetry of the circuit, we can see that v_E remains constant for a pure differential mode input.

      Therefore to get a downward 2 V swing, v_C needs to go to 11 V and v_E should be no higher than 10.5 V to avoid saturation. v_E follows v_i, so when the input common mode voltage goes to +2.5 V, v_E will be 2.5 V above the Q point.

   3. However, we also need to accommodate a ±2.5 V common-mode or average input v_c = [((v_i+v_i^¢))/ 2], while maintaining our output voltage swing limits. This means that the highest input on the base will be 5.0 V above the lowest voltage on the base.

   4. The drop across R_E is only 2 mA×47 ohms » 0.1 V, so we want v_A £ 8 V at the Q point. Since the Q point current in R₁ is 4 mA, R₁ = [8 volt/ 4 mA] » 2 k. However, our 10% resistors have standard values of 1.0, 1.2, 1.5, 1.8, 2.2. 2.7, with any multiplier, so we choose the nearest standard value of resistor on the low side which is 1.8 k.

V_B = ____________  V.

V_B^¢ = ____________  V. V_E = ____________  V.

V_E^¢ = ____________  V. V_A = ____________  V. V_C = ____________  V.

V_C^¢ = ____________  V. The bias network must now supply the appropriate V_B. We have a voltage for V_B of
V_E = 4 mA× 1.8 K (about 0.1 V across R_E) +0.7 V » 8 V. This gives the required ratio for R_H and R_L assuming that b®¥.

To allow for b_min = 75, we must limit the Thevenin impedance of the voltage divider. If we want the maximum change in the emitter Q point to be 0.2 V, then I_B =2 mA/75 through the Thevenin impedance must produce a voltage drop of less than 0.2 V.

Use these values to calculate R_H and R_L and then choose the closest available values from the list of standard resistor values. R_H = ____________  ohm

R_L = ____________  ohm Calculate the expected A_c and A_d using the actual resistor values. A_c = ____________

A_d = ____________