Answer the questions 1 through 15 in this writeup before coming to the lab. They will be collected at the beginning of the lab. Read the sections of the text referenced here, if you haven't already.

1  Purpose

• To look at one type of fundamental noise: Johnson noise or thermal noise voltage that appears across every resistor or any other device that can dissipate power.

• Then, in the next lab, to try out one powerful technique for measuring small signals in the presence of noise: the phase detector, or lock in amplifier.

2   Introduction

The Johnson noise voltage ``spectral density'' that appears across a resistor is e_n = [Ö(4k_BTR)]. (See sections 7.11-7.14; pp 430-443 in Horowitz-Hill 2^nd edition.) For a 1M resistor at room temperature (300 K) e_n = 1.3 ×10^-7  V/[ÖHz], or ~ 4 mV rms in a 1 KHz bandwidth. We will, therefore, need a high gain amplifier whose intrinsic noise is small so that it does not cover up the thermal noise from the resistor.

3  Procedure

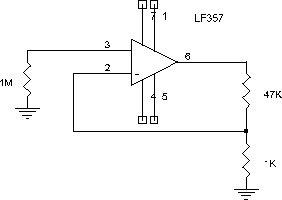
For the first amplifier stage, start near the left edge of the upper breadboard block (to the left of your tuned amplifier) and wire the following circuit:

Figure 1:

Clip the component leads short and bend them so the component bodies lie flat against the breadboard - this minimizes stray capacitances. Use a single bus on the socket for all the grounds (probably the inner strip below the op-amp). It is a good idea to put 0.1 mF capacitors from the +15 V and the -15 V supply pins of each op-amp to ground to bypass the power supply.

The LF357 is an inexpensive op-amp with JFET input transistors and reasonably low noise. Use information from the spec sheet to find the following.

[Question 1] What is the gain of this stage (measured from the + input)?

[Question 2] The voltage noise spectral density (e_n) at the input due to the op-amp voltage noise? Use values for f ~ 1 kHz.

[Question 3] The voltage noise spectral density at the input due to the op-amp current noise (i_n) (for the circuit with R_in = 1M)?

[Question 4] The total voltage noise at the input from these two amplifier-related sources (remember that independent random voltages add in quadrature!)?

[Question 5] The noise temperature of this op-amp with R_in = 1M?

[Question 6] The noise figure for the op-amp with R_in = 1M? (See Section 7.12 in Horowitz-Hill, 2nd edition.)

[Question 7] The noise resistance of the op-amp?

[Questions 8] Repeat 2) through 7) for an OP-27 ultra-low noise bipolar input op-amp:
e_n = 3 nV/[ÖHz], i_n = 0.4 pA/[ÖHz].

[Question 9] Which is the better op-amp for this application?

Since we will use the DVM to measure an rms voltage, v_rms, we need to define a bandwidth so that this voltage can be predicted from the Johnson noise spectral density, e_n.

Now refer to your previous laboratory (Operational Amplifiers) and consider the three stage tuned amplifier that you previously constructed on the right side of the top block of the breadboard.

[Question 10] What is f_°, the center of the bandpass? (As usual, remember the difference between f(Hz) and w(rad/sec))

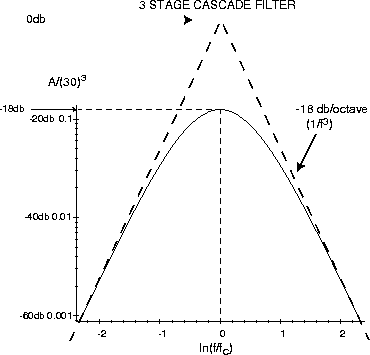
The use of the three stages results in a better definition of the bandwidth and reduces the gain at 60 Hz ( << f_°) to the point where we have some hope of operating a completely unshielded high gain circuit like this in the presence of the large line-frequency fields in the laboratory. The overall gain is sketched below:

Figure 2:

[Question 11] What is the gain of the three stage amplifier at f=60 Hz?

[Question 12] How many db down from the peak gain is this?

[Power levels, such as 30 watt or 40 watt, are often compared by taking the logarithm of the ratio of the Power levels. When comparing two power levels P_a and P_b, we might generate
n = log₁₀([(P_a)/( P_b)])
and say the ``Power difference is n bels''.  More usually, we generate
m = 10.0 log<sub>10</sub>([(P<sub>a</sub>)/( P<sub>b</sub>)])
and we say the ``Power difference is m decibels'' or ``a is m db above b''. When comparing voltages, across identical resistors R, then the ratio of the powers in the resistors is related to the ratio of the voltages.
m = 10.0 log₁₀([(P_a)/( P_b)]) = 10.0 log₁₀([(V²_a/R)/( V²_b/R)])    = 20.0 log₁₀([(V_a)/( V_b)])

For example, if the voltage V_a at a is twice the voltage V_b at b, then
m = 20.0 log₁₀(²/₁) = 20.0×(0.3010) = 6.02
and we say that ``the voltage at a is 6 decibels or 6 db above the voltage at b''. Note that this applies only if the two systems have the same impedance to ground. Perhaps both signals are moving in 50 ohm transmission lines.

One can compare voltage gains in the same way as comparing voltages. For example, if a voltage gain is increased two-fold, then it has been raised by 6 db.]

Now we need to calculate the rms output voltage we expect for a given voltage spectral density at the input. We will assume ``white noise'', where the spectral density, e_n is independent of frequency. The rms input voltage in a bandwidth df at any frequency f is then e_n [Ödf], and the output voltage is A(f)e_n[Ödf] . We must add these voltages for all frequencies where we have any gain, but since the phases are random and independent, we must add their squares:

[Question 13] Show that:

vrms = en é ê ë (1st stage gain)(303) æ è   æ Ö f°   ö ø æ ç è ¥ ó õ °  é ê ë x 1+x2 ù ú û 6   dx ö ÷ ø 1/2   ù ú û

[Question 14] Given that

¥ ó õ °  æ ç è x 1+x2 ö ÷ ø 6   dx = 3p 512

find the numerical value for k such that v_rms-out = ke_n.

The peak gain of the tuned stages is quite sensitive to the exact values of the capacitors. If you want accurate results, it would be a good idea to remeasure the net gain of the three tuned stages at the frequency where it is maximum, and scale your calculated k to the extent that the measure value differs from 30³/8. To do this, we use a sine wave from the signal generator as a source, inserting the ¸100 and ¸10 attenuators in order to set to a sufficiently low voltage. It is best to use your scope to measure the input and output voltages.

• Adjust the frequency for maximum output (note the frequency, but don't worry if it differs slightly from the calculated f_° . If you must use the DVM to measure the input and output voltage to get the gain, be sure to properly subtract the input and output noise readings when the attenuators are disconnected from the generator.

• Just to check the noise contribution from the 741 stages, temporarily ground the input of the first tuned stage (make sure it is disconnected from the low-impedance LM357 stage output!!) and measure the rms output voltage of the last stage with the DVM - record your values.

• Now connect the first tuned stage input to the output of the LM357. Temporarily short the 1M resistor to ground the input. Measure the output voltage. Subtract the contribution from the 741 stages (in quadrature) to get the noise due to the 357 stage only.

• Is the correction significant? Use the result of Ques. 14 to convert your rms voltage to a spectral density at the input. How well does this agree with e_n from the data sheet?

• Now remove the short from the resistor and again measure the output voltage. You can subtract the total (input shorted) amplifier noise. Is the correction significant? This does not correct for the amplifier current noise, - (Why not?) - but the current noise is unlikely to be significant for R_in = 1M or less. Convert this to e_n for the resistor. How does it compare to [Ö4kTR]? (300 K is close enough to room temperature.)

• Be sure to look at the output on the scope as well as on the DVM. It should look like random noise. If it doesn't seem right, check with the instructor.

• Get a 200 K metal film resistor mounted on a short shielded tube (from the instructor, if it is not on your bench!) and substitute it for the 1M resistor. Which side of the resistor should be connected to ground? What value do you get for e_n noise? Does it scale as you expect with R?

• The resistance of metal alloys, such as the nichrome film in these resistors, is essentially independent of temperature at room temperature and below. We can therefore cool the resistor and check the expected T dependence of Johnson noise. Nest two Styrofoam coffee cups and fill the inner one with liquid nitrogen (LN₂, T = 77 K) from the dewar in the lab. Don't spill it in your shoes! (If you have never handled LN₂ before, you may want to ask the instructor to do it for you!) Immerse ~ 2 cm of the end of the tube in the LN₂. (The resistance of a carbon composition resistor would almost double, if you used one here.)

• After things settle down, check the scope to see it the ``popcorn'' due to mechanical contraction in the resistor has pretty much stopped. When it has, take a reading from the DVM and calculate e_n. Don't forget to correct for amplifier noise - it's starting to get important at these low levels.)

[Question 15] By what factor did you expect it to drop?

Note: save your breadboard in the cabinet again - you will use it for the Phase Detector Lab next week.

You will use your 3-stage tuned amplifier and low-noise input stage from the Johnson Noise lab. Construct the following circuit on the lower breadboard block as far to the right as possible (to keep it away from the 357 input). Be sure the square wave input comes in from the right side of the breadboard. (You should not be using either of the BNC connectors on the left.)

(You can use any one of the six devices on the 7404 chip. Note that it requires connections to ground and to V_cc = 5 V. Note also that the HI-300 requires a ground connection for input reference control. )

Figure 3:

Set the pulse generator to give a 0-4V square wave output at a frequency near f_°. Replace the resistor at the amplifier input with a 1 K and add a photodiode as shown below:

Figure 4:

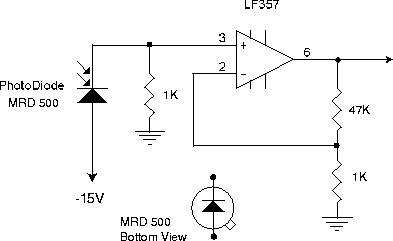
Put a ~ 25 mm piece of black tubing over the end or your photodiode to limit the amount of background light that strikes it. Bend the leads so it is aimed nearly horizontally of the left end of your breadboard, trying to point it a a part of the room that is not too bright (set up a dark screen, if necessary). Put a red LED in series with a 100 ohm resistor at the end of a coax cable and connect it also to the pulse output.

Figure 5:

• Look at the amplifier output on the scope. Push the LED into the end of the black tube on the photodiode adjust the distance to give an output that is large, but not close to saturating (ie   ~ 4-18 V p-p). Adjust the frequency for maximum amplitude (at f_°). The output will be a sine wave, even though you are driving the LED with a square wave. If the amplitude is too large, reduce the light response by replacing the 1 K resistor on the + input with a smaller value.

  [Question 1] Why? (Hint; think of the Fourier analysis of square waves!)

• Look at the signal on the output of the broadband 357 stage. Now look at the output of the phase detector switch at point A. Lock-in amplifiers usually have some provision for adjusting the phase of the reference relative to the signal. We will cheat and use the rapid change of phase with frequency of the signal while the reference (switching) phase remains constant. Try adjusting the frequency while watching point A. (Be sure the scope is DC coupled!) Sketch what you see.
• Guess how the average voltage at A changes as you change the phase, then look at the output of the low-pass filter at B. (Unfortunately, the amplitude also changes as you change the frequency and you will have to allow for this.) Use a 10× probe to look at point B so you don't load the filter too much. Set the frequency back to f_° to give zero phase shift.

• Now replace the 1K resistor with a 1M resistor and remove the LED. This will increase the light sensitivity by a factor of 1000. Looking at the amplifier output on the scope, you will see the Johnson noise of the 1M resistor, plus some 60 Hz hash from the room lights. If the output is saturating at any time due to pick-up, try placing a small piece (5 cm × 5 cm) of grounded Aluminum foil in such a way as to shield the input circuit. Check the output of the LM357 stage with the DC-coupled scope to be sure that it isn't saturating from ambient light. Set up shields or aim the tubing as necessary to keep the output of the amplifier last stage from saturating. Bring the LED near the end of the photodiode tube, while looking at the amplifier output (or point A). Note the high sensitivity - but also the large amount of noise. Now look at the filter output (point B) on the other scope channel.

• Set the scope gain to 20 mV/cm (that's 2 mV on your dial - you're using a 10× probe, remember?). Note the noise level.

[Question 2] What rms fluctuation do you expect in the output of this filter due to the Johnson noise in the 1M resistor?
(Forget your integral over the tuned amplifier gain now - your gain(f) is almost a delta function at f_°. The width is 2× the bandwidth of the low-pass filter: BW = [(p)/2][1/(2pRC)]. The effective bandwidth is smaller than this by 1/2, since noise components 90^° out of phase with the reference don't give any output - even though they are at the correct frequency.)

• Try holding your hand in front of the photodiode and then shining the LED on your palm.
• Can you see the shift at point B?
• Can you see the light on your hand?
• Can you see the signal at point A?