1  Purpose

• To understand the basic concepts and characteristics of an ideal operational amplifier.

• To compare the characteristics of a high performance low cost IC op amp with those of the ideal.

• To investigate the properties of the IC op amp in several circuits which demonstrate its great versatility and range of operation.
• Note that this is a two-week lab. You should be able to complete through part 4 or part 5 during the first week.

2  Discussion

Modern integrated circuit operational amplifiers (op amps) have characteristics so closely approaching the ideal op amp that they are components of almost all signal processing and instrumentation equipment. The properties of a commonly used 741 op amp are compared to the ideal values listed in the table below:

Parameter	Ideal Value	mA741 Value	1990 best avail. value
			(not all in same device)
Input current	Iin = 0	~ 80 nA	0.1 pA
Voltage gain	Av = ¥	200,000	2×106
Bandwidth	BW = ¥	1 MHz at Av = 1	500 MHz
Balance	Vo = 0 for Vi = 0	Vo = 0 at Vi = 1-2 mV	5 mV
Temperature	none	(dV/dT)offset typically	(dV/dT)offset 0.1 mV/C
dependence		15 mV/° C

Op amps can be obtained commercially for $0.50 to $3.00 each. This and their versatility are the reasons for their great popularity. As you perform the suggested investigations, be alert to observe and note those cases in which the real op amp fails to match the ideal properties. Try to find the relevant properties in the ``spec sheets'', and take note of the ``typical applications'' section - this is a prime spot for getting circuit ideas or finding out how new devices might be used.

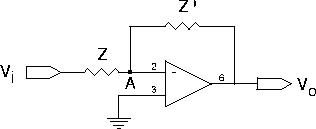
Almost all applications of op amps involve negative feedback as indicated in the diagram below:

Figure 1:

Assume that point A is a virtual ground (i.e. V_- = V₊), and that I_i = 0, and prove the general result that

3  Procedure

• For each circuit you will test, first draw a schematic diagram in your lab notebook, that includes IC pin numbers for the integrated circuit (obtainable from the specification sheets). As you can see from the circuits in this handout, it is customary not to show the power supply connections or bypassing, so simply add a diagram at the beginning to show these connections, which can be left in place for the remainder of the single Op-Amp experiments.

• Near the supply pins (±15 V), connect filter capacitors (0.01  mF) to ground.

• Where appropriate in the exercises listed below, compare the measured gain A and frequency response to the values listed on the specification sheets.

1. Connect the op amp as an ordinary amplifier as shown below.
   • Find the ``output voltage swing'' and the ``slew rate'' specifications on the data sheet and determine what they mean.
   • Can you measure them?
   • Check the magnitude and phase of the gain.
   • Measure the bandwidth and the input impedance at the V_in terminals. (The insertion of the R_test resistor is useful in determining the input impedance.)
   
   Figure 2:

2. Connect the op amp as a non-inverting amplifier.

   • Confirm the magnitude and phase of the gain.
   • What is the input impedance in this configuration?
   
   Figure 3:

3. Construct an adder. Verify, using three or four pairs of input values, that:

   Vo = - ( v1 + v2 )

   It is most convenient to use the square blue 10k potentiometers with pins on the back side as adjustable voltage sources for v₁ and v₂.
   
   Figure 4:

4. As shown below, connect the op amp as an integrator. Use positive pulses 1 msec wide at a frequency of 40 Hz as the input.

   • Observe the input and output using the ALT or CHOP mode scope inputs on DC. Because of the 100k resistor, this is not a true integrator, but is referred to as a leaky integrator.
   • What is the effect of the resistor?
   
   Figure 5:

5. Now modify the integrator to be a charge sensitive amplifier. This is the electronic analog of a ballistic galvanometer.

   • Charge a 0.1 m F capacitor on the +15 V supply.
   • Connect it to the inverting input.
   • Derive the equation:

     V° = - 1 Cf ó õ iin dt = - Qin Cf

   • Experimentally confirm it with your measurement.
   • Try another value of input capacitance and note whether the peak value of V_out tracks the input charge.
   
   Figure 6:

6. Construct a logarithmic amplifier as shown below.

   • Vary V_in and plot V_o = A + B ln V_i using a semi-log scale. Five or six values are sufficient - be sure they cover a wide range in V₀. (You can use the Log functions on your calculator and the ruled paper in your notebook for the plot.)
   • Does it make any sense to use an AC input voltage for this measurement?
   • What are your values of A and B?
   
   Figure 7:

7. Note that, while an Op-Amp has differential inputs, the gain stabilized amplifier circuits in parts 1 and 2 above do not.

   • To gain the advantages of a differential input with an accurate gain and good common mode rejection, construct the Instrumentation Amplifier as shown below.

   • Understand out how it works.

   • Try a few combinations of v⁺_in and v^-_in to find the differential and common mode gains.
   
   Figure 8:

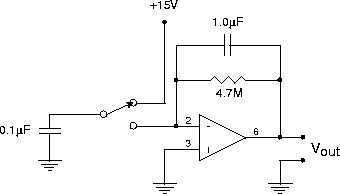
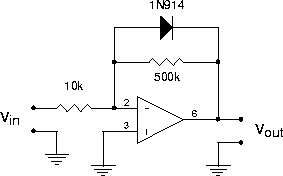
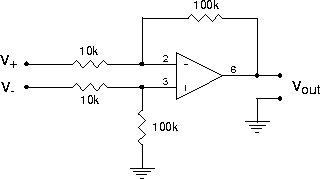
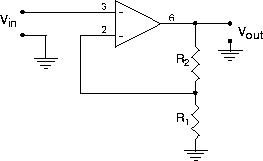
   (This particular circuit has several drawbacks. Check Horowitz & Hill for a nifty ``3 Op-Amp Instrumentation Amplifier'' that has:

   • a CMRR over 100,000
   • an essentially infinite input impedance on both inputs
   • gain that is adjustable over a wide range by changing one resistor.)

8. The final circuit will be used in the next lab, so build it on the circuit board that is marked with your name and save it. This is a high gain circuit and some care in the layout is needed; the instructor should have an example to show you before you start.

   The circuit consists of three identical stages, which should be arranged from left to right across the upper breadboard block, leaving about 1/3 of the block free on the left. Clip the component leads short and bend them with your pliers so that the component bodies lie flat against the breadboard - this minimizes stray capacitances. Use a single bus on the socket for all the grounds - for example, the inner strip just below the op amps. It is a good idea to put 0.1 mF ceramic capacitors from the ± 15 V supply pins to the ground bus as close as possible to each op-amp. The instructor will show you a sample layout before you start.

   The circuit for a single tuned amplifier stage is:

   
   Figure 9:

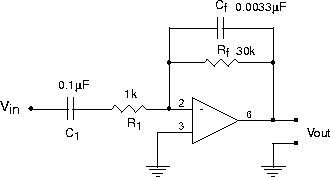
   Ignoring the capacitors for a moment, this is just an inverting amplifier with a gain of R_F/R₁ = 30. The addition of C₁ introduces a high-pass corner at f₁ = 1/2pR₁C₁ that reduces the gain at low frequencies, ie f << f₁:

   
   Figure 10:

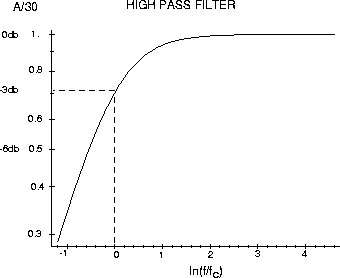
   The addition of C_f reduces the gain at high frequencies, i.e. f₂ = 1/2pR_fC_f

   
   Figure 11:

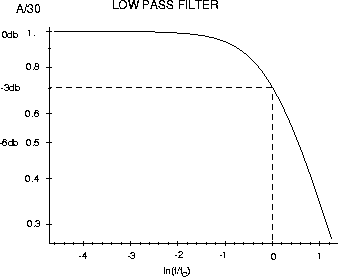
   With both capacitors, the gain is just the product of these two curves. Since f₁ = f₂ º f_°, the result is :

   
   Figure 12:

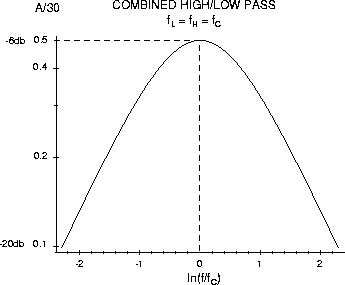
   Therefore, the maximum gain of the stage is 1/2 (R₁/R_F) = 15 at f_°, and drops off µ f for f << f_° and as 1/f for f >> f_° - both 6 db per octave. What is f_° for the given component values?

   To make a high gain amplifier with a fairly narrow bandwidth, we cascade three (3) identical stages. The gain is then:

   Av = ( 30 )3 æ ç è f/f° 1+(f/f°)2 ö ÷ ø 3

   The peak gain is now A_v = 30³/8 = 3375 at f = f_° and drops off as 1/f³ for f >> f_° , and as f³ for f << f_°.
   
   Figure 13:
   • Construct the three stage amplifier;
   • measure the frequency at which the gain is maximum; and
   • record the gain at this frequency.

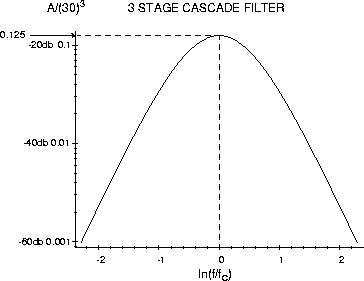
   • How does the frequency of peak gain compare to your calculated f_°? (For the input signal, use the 100 × attenuator on the wave-form generator output). Measure the input and output voltage with a scope, not the DVM.
     You can use the DVM if you are careful to take the noise into account. How do you do this?

   • Plot the frequency response (logA_v vs. logw from ~ 50 Hz to 50 kHz with about 3 points per decade. (This implies about a factor of 2 between points to be about evenly spaced on the logarithmic scale.)
   • Record the value at 60 Hz.