1  Purpose

2  Discussion

The investigations are made on the circuit breadboard as usual. Use the 741 Op-amp which you used in earlier investigations. Start the circuit by placing the op-amp on the right side of the breadboard. It is suggested that, when necessary build the Wein bridge to the right of the op-amp and the stabilizing circuit to the left.

3  Procedure

Figure 1:

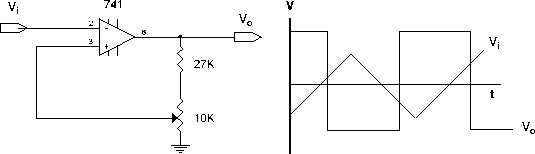
Study the behavior of the circuit as you vary the amount of positive feedback. Explain carefully in your lab book why the circuit switches from one state to the other at a particular value of the input voltage. Keep the Wavetek set to low frequencies ( ~ 25 Hz). Measure this switching voltage using the ``chop'' mode on the scope. The low frequency is necessary because of the slow overload recovery time ( ~ 1 msec). Try a relaxation oscillator as shown in Figure 2. Calculate the oscillator frequency from the circuit component values. Observe the waveforms at the output and at both inputs. Write an explanation of the operation of the circuit.

Figure 2:

Make a Wein bridge oscillator with gain A, adjustable with a 10K pot as shown in the circuit of Figure 3. The particular component values are only suggested and you can equally well use similar values. Attempt to obtain a non-saturated sinusoidal output and note the relative ease or difficulty you find in achieving this.

Figure 3:

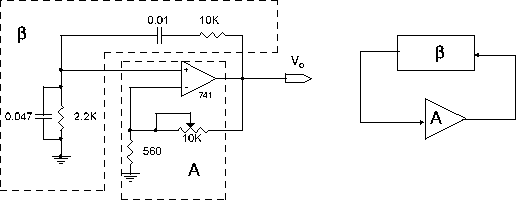
Now use the transistor as a stabilizing element. In the circuit shown in Figure 4, the diode rectifies the output voltage and biases the FET so that its drain to source resistance become larger, reducing the amplifier gain A. Vary the 10K pot and observe how well (or poorly) the circuit performs, particularly in comparison to the unstabilized configuration. Adjust the circuit for » 2V p-p oscillations by adjusting the 10K pot. Then put your finger on the FET to heat it slightly and observe any changes which occur in the level of oscillation.

Figure 4:

4  Questions

1. Calculate the period of the relaxation oscillator in Fig. 2 for arbitrary values of the parameters. Denote the R and C in the negative feedback loop as R and C, and let the fraction of the output voltage fed back as positive feedback be denoted as b. Then evaluate the period for the component values specified in the circuit. Assume the 10K pot is set to the maximum (arrow at the top).

2. On a single graph, plot V_out, V₊, and V_- as functions of time. Note that labeling the time axis in units of RC gives the answer to 1) above. You can assume any starting point you like, eg V_C = V_- = 0, V_out = high (+14 V).

3. For the Wien bridge in Fig. 3, calculate the feedback ratio (b º [(V₊)/( V_out)]) as a function of frequency (use of complex impedances is best). Determine the frequency w₀, at which oscillations will occur. What is the value of b at this point? What minimum gain A is required for oscillation?