| 9.6, 9.8: "Show directly" in these problems means "show without using a generating function", that is, by using the Jacobian matrix or the fundamental Poisson bracket relations. Use different methods in the two problems so you see how both work. | ||
Note: The generating functions in Prob. 9.8: are of mixed type, not of types 1-4 in Goldstein's classification. All that is required is that F depend on two of the initial variables and two of the final variables. The choice must be such that it is possible to solve the starting relations for the remaining variables. Note that in integrating the differential relation which gives a variable in terms of the derivative of F with respect to its conjugate variable, it is necessary to allow "constants of integration" which are functions of the remaining independent variables. |
||
|
9.14: The Lagrangian for the problem is L =
½ mv² + ev· A/c with
A = ½B × r.
9.32: The series can also be written as exp(-t 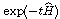 ) where ) where
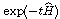 is the differential operator defined by writing
the Poisson bracket as is the differential operator defined by writing
the Poisson bracket as 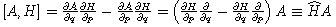 . . This structure appears frequently in the quantum context. Try it! |

| LD19(a): The canonical transformation in part (a) is an
identity transformation for the coordinates and momenta qj,
pj with j > 1. Only the relevant part of the generating
function is given.
LD19(b): The constants Li,j correspond to rotations in the i,j plane. They were derived for the q's in the Lagrangian setting in LD6, Problem Set 3. The effect of the full set of transformations on the q's and p's, and the fact that the q's and p's can be interchanged canonically as in (a), should suggest why the "extra" constants of the motion Qi,j exist. The set of N2 - 1 constants Li,j and Qi,j independent of the Hamiltonian generate the symmetry group SU(N) of the isotropic N-dimensional oscillator. |
Send comments or questions to: ldurand@hep.wisc.edu
FURTHER OPTIONS:
- WHAT'S NEW
- COURSE INFORMATION
- SYLLABUS
- HOMEWORK ASSIGNMENTS
- EXAMS
© 1997, 1998, Loyal Durand