
PROBLEM SET 6
Due Friday, March 10, 2006
Reading: Landau and Lifshitz, Secs. 30, 33, 78, 79

Comment: Think about how you would derive the expression
given for Y. The statistical weight 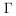 is simply a counting factor with is simply a counting factor with 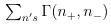 playing the role of a phase space integration. You will need to introduce probabilities wl with which different values of l enter, then determine them using Gibbs' construction
and maximizing the Gibbs information entropy subject to the constraints on the average length and the normalization condition. The tension
appears in the Lagrange multiplier factor and can be identified using
the first law dE = TdS - dW with dW = - playing the role of a phase space integration. You will need to introduce probabilities wl with which different values of l enter, then determine them using Gibbs' construction
and maximizing the Gibbs information entropy subject to the constraints on the average length and the normalization condition. The tension
appears in the Lagrange multiplier factor and can be identified using
the first law dE = TdS - dW with dW = -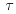 dl
the work done by the tension when l is changed by an amount
dl. A
Legendre transform from S, l to T, dl
the work done by the tension when l is changed by an amount
dl. A
Legendre transform from S, l to T, 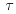 as the independent variables gives the first law in the form
dG = -SdT - l
as the independent variables gives the first law in the form
dG = -SdT - l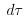 . We then identify
G(T, . We then identify
G(T,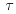 ) with -kTlnY
in the usual way. ) with -kTlnY
in the usual way.
|

| Hint: Expand the exponential in the expression for b2 to order ( V1,2/kT)2, then integrate first over the directions of p1 and p2, noting terms that vanish. The final integral over the direction of r is simple.
Comment on how the temperature dependence of this result differs from that obtained for a scalar potential V(r). |

| Comment:
This calculation completes the work done in LD14
on the equation of state
for a neutral plasma of electrons and singly charges ions. The difficulty that
appeared there was one characteristic of long-range forces: one could not
calculate the Coulomb energy by
averaging in the free particle distribution, or use the cluster expansion,
because the integrals diverge in both cases. Yet it is clear physically that
a chunk of plasma will appear to be neutral on the average when viewed from
a distance. The solution to the problem is to reformulate the expression for
the Coulomb energy in terms of the radial distribution functions of electrons
and ions around each particle. The average neutrality of the plasma and the
correlations (shielding) near each particle can then be taken into account
in the Debye-Hückel approximation. These two steps are the essence of
this problem.
It is not trivial to go beyond the Debye-Hückel approximation. Divergent integrals appear in a naive expansion of the Boltzmann factor because of the Coulomb singularity, and it is necessary to include quantum mechanical corrections to eliminate them. See L. S. Brown and L. G. Yaffe, Physics Reports 340, 1-164 (2001). The length of the paper indicates the subtlety of the calculations involved. |

| Comment: The calculations are straightforward except for (ii) where you will need to use the Schwarz inequality for sums or complex vectors. In all parts, keep in mind the normalization conditions, and be careful with the complex conjugates - there is a tendency to want to switch the factors with the *. |