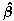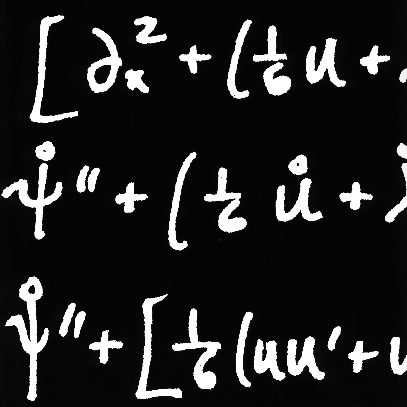
Hint: In the addition to 11.10(b), show that the matrix you obtain agrees with Eq. 11.98, then consider the action of the matrix on a four vector x to get x', determine the components to the latter, and compare with the expression in Eq. 11.19.

The effect of the 2.75 K black body background radiation on the cosmic ray spectrum was first discussed by K. Greisen, Phys. Rev. Letters 16, 748 (1966) and by G.T. Zatsepin and V.A. Kuz'min, Sov. Phys. JETP Letters 4, 78 (1966). The limits present a problem in explaining the origin of the highest energy cosmic rays observed.

In part (ii), you will want to find the tangent of the scattering angle. The hyperbolic results are simple. To relate them to the results in Jackson, rewrite them in terms of velocities and 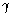factors and use the relation between v² and 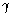².

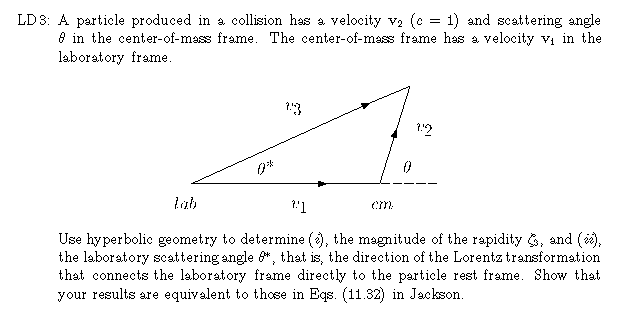
Particle distributions in high-energy collider detectors are commonly plotted in terms of 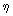and the azimuthal angle 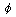around the beam direction. The maximum energy of pions produced in the Fermilab proton-antiproton collider is 900 GeV, corresponding to a true rapidity 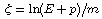equal to 9.5, with most particles at considerably small values. While the psuedorapidity diverges for vanishing transverse momentum (small angles), the approximation 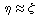breaks down when the transverse momentum is small relative to the particle mass. The difference is generally not important practically.

Send comments or questions to: ldurand@theory2.physics.wisc.edu

FURTHER OPTIONS:

© 1997, 1998 Loyal Durand