Problems: LD 18, LD 19

Parts (a) and (c) in this problem show the difference between the mechanical momentum density of an elastic solid defined as the product of the local mass density and velocity, 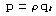, and the momentum density associated with waves in the solid. The equation of motion, or flow equation for the mechanical momentum, states that the Noether current associated with rigid translations of q is conserved. The conservation of the energy-momentum tensor, in constrast, follows from Noether's theorem and the invariance of the action under rigid translations of the coordinates x. The energy density in the waves is H = T00, while P = T0i.

The one-kink solution corresponds to a single twist in the long chain of coupled pendula treated in the mechanical model in LD 12. For an infinite chain, or a chain with the ends clamped, there is no way to undo the twist through oscillations of the pendula. The topologies of the twisted and untwisted chains are different. The sine-Gordon equation has an infinite set of twist solutions with distict topologies specified by the total twist, positive or negative, between the endpoints. These have finite total energies as here, with the energy density localized near the twists. The moving excitations are called "solitons". Alwyn Scott, formerly in Engineering at UW, built a mechanical model of the type discussed. It was possible to see the Lorentz contraction of the kink as its speed was increased. Relativity works!

Send comments or questions to: ldurand@theory2.physics.wisc.edu

FURTHER OPTIONS:

© 1997, 1998, 1999 Loyal Durand