This is an example of a Hamiltonian that depends explicitly on the time. Note that p is the canonical momentum of the damped oscillator, not its velocity. This difference is crucial in Liouville's theorem.

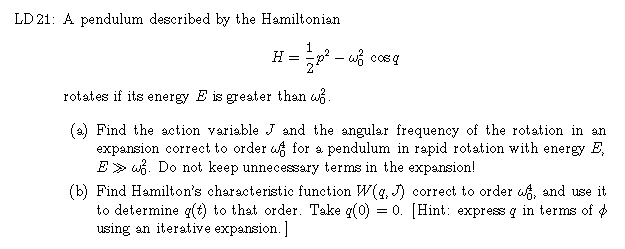
Take the hints seriously! In (a), expand the expression for J in inverse powers of E before integrating, and continue expanding as appropriate. You will need to invert the expression approximately to find E(J) which you can then use to find 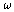. In (b) you will need to use W(q,J) to get an expression for 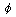as a function of q and J. Rewrite it as q = 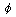+ ..., substitute repeatedly for q in terms of 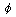the terms in the ellipsis, and expand in the small parameter to obtain the iterative solution for q.

There is a subtlety in this problem: the solution for the initial condition q(0) = 0 can (and will) involve 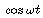as well as 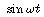. This is possible because the general Fourier series includes a constant term a0 that can be used to cancel the unwanted contribution from the cosine at t = 0. The actual calculation is straightforward, but can be messy if you do not think ahead about the potential sizes of the various terms in the Fourier series. A useful approach is to assume that all coefficients in the general Fourier series are smaller than the coefficient of the leading term that satisfies the initial condition, namely q = b1, by at least one power of , and substitute the general series in the equation of motion and expand to order to see what further harmonics must be present in the solution at that order. The process can then be repeated with the new starting solution to go to higher order. Give your arguments about which terms can be large, and show that your assumptions are consistent by showing that your proposed solution actually satisfies the equation of motion and the initial condition to the order requested.

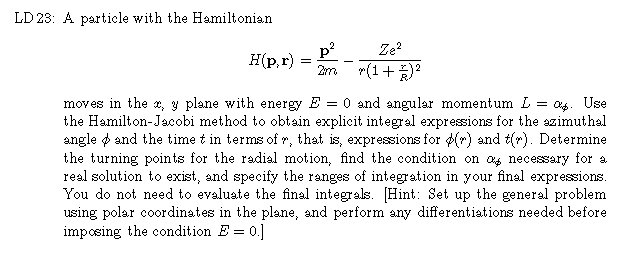
Carry the calculation through to the point at which you have explicit integral expressions for the time and angle as functions of r. Find the turning points in the radial motion, determine the limit on 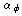that is necessary for a real solution to exist, and specify your range of integration. You do not need to evaluate the final integrals. They can be evaluated in closed form, but the results are not especially illuminating. However, you may wish to show that the E = 0 orbits close by calculating the change in 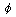over one radial oscillation. The potential in this example gives a very good approximation to the Fermi-Dirac statistical potential for electrons in an atom. The last electron in the neutral atom has a binding energy that is very small on the scale of the average atomic energies, and is taken as zero in the statistical model. Thus, you are calculating a reasonable approximation to the classical orbit of the last electron in a large atom. The angular momentum of this electron is limited as you found. The potential also has the interesting property of belonging to a class of "focussing potentials" with optical analogs. See Demkov and Ostrovskii, Soviet Phys. (JETP) 33, 1083 (1971).

Send comments or questions to: ldurand@theory2.physics.wisc.edu

FURTHER OPTIONS:

© 1997, 1998, 1999 Loyal Durand