PROBLEM SET 12

Due Wednesday, May 5, 1999

Problems: LD 24-26

FINAL EXAM MONDAY, MAY 10, AT 12:25 PM . EMPHASIS ON CLASSICAL MECHANICS AND FIELDS, GOLDSTEIN CHAPS. 10-12, LECTURE MATERIAL

   This problem makes extensive use of the material on the Kepler problem given in Goldstein. See Secs. 10.7 (the use of action-angle variables and the elimination of degeneracies) and 3.7 (explicit solution). You will want to use the fact that the angular momentum perpendicular to the plane is a constant of the motion and take J2 = L, where E = E(J1). 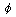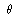Rewrite the integral of the perturbing Hamiltonian over over the angle variable 1, first as a time integral, and then as an integral using the relation dt = mr2d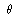/L. Use the explicit solution of the unperturbed Kepler problem to evaluate that integral. It is then straightforward to find the new angular frequencies.

   Start the perturbation calculation in (b) with the uncoupled problem defined by setting 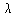= 0.

In the case that the two original frequencies are degenerate, the unperturbed Hamiltonian can be expressed in terms of a single action variable J = J1 + J2. What happens in this case?

   See Arnol'd, Sec. 25, for the formal background material. One can determine the stability of a system with a "frequency" 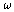2(t) by repeated mapping of the initial point z0 = z(0) in phase space back to the (same) phase space at times nT, n = 1,2,... Determine the 2× 2 matrix gT that gives z(T) = gTz0 after one period T of the "frequency". The motion is stable and gTnz0 remains close to z0 if the real parts of the eigenvalues of gT have magnitudes less than 1. This requires that Tr gT < 2 in the present 2× 2 case. So find gT (this is easiest to do by finding the matrices for the first and second halves of the motion, and multiplying them), calculate the trace, and apply the condition given. A sketch of even the stable motion will produce a wild-looking curve of the type you will see in discussions of particle motion in accelerators.

Send comments or questions to: ldurand@theory2.physics.wisc.edu

FURTHER OPTIONS:

© 1997, 1998, 1999 Loyal Durand