 |
|
This method was used to determine the parity of the 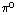 ,
but with a variation: A virtual high-energy photon can convert to an
electron-positron pair (a "Dalitz pair") with a probability of about 1/170.
The charged particles tend to lie in the plane of E (why?), so by
looking at the correlation of the planes of double Dalitz pairs in the
decay ,
but with a variation: A virtual high-energy photon can convert to an
electron-positron pair (a "Dalitz pair") with a probability of about 1/170.
The charged particles tend to lie in the plane of E (why?), so by
looking at the correlation of the planes of double Dalitz pairs in the
decay 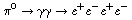 , one can measure the correlation of the
photon polarizations and determine the parity of the , one can measure the correlation of the
photon polarizations and determine the parity of the
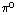 .
For some original references see C.N. Yang, Phys. Rev. 77, 242, 722
(1950); N. Kroll and W. Wada, Phys. Rev. 98, 1355 (1955); and for
the original measurement, R. Plano et al., Phys. Rev. Lett.
3, 525 (1959). .
For some original references see C.N. Yang, Phys. Rev. 77, 242, 722
(1950); N. Kroll and W. Wada, Phys. Rev. 98, 1355 (1955); and for
the original measurement, R. Plano et al., Phys. Rev. Lett.
3, 525 (1959).
|

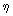 and the azimuthal angle
and the azimuthal angle
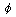 around the beam direction. The maximum energy of pions
produced in the Fermilab proton-antiproton collider is 900 GeV, corresponding
to a true rapidity
around the beam direction. The maximum energy of pions
produced in the Fermilab proton-antiproton collider is 900 GeV, corresponding
to a true rapidity 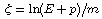 equal to 9.5, with most particles
at considerably small values. While the psuedorapidity diverges for
vanishing transverse momentum (small angles),
the approximation
equal to 9.5, with most particles
at considerably small values. While the psuedorapidity diverges for
vanishing transverse momentum (small angles),
the approximation 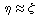 breaks down when the transverse momentum is small
relative to the particle mass. The difference is generally not important
practically.
breaks down when the transverse momentum is small
relative to the particle mass. The difference is generally not important
practically.


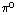 ,
but with a variation: A virtual high-energy photon can convert to an
electron-positron pair (a "Dalitz pair") with a probability of about 1/170.
The charged particles tend to lie in the plane of E (why?), so by
looking at the correlation of the planes of double Dalitz pairs in the
decay
,
but with a variation: A virtual high-energy photon can convert to an
electron-positron pair (a "Dalitz pair") with a probability of about 1/170.
The charged particles tend to lie in the plane of E (why?), so by
looking at the correlation of the planes of double Dalitz pairs in the
decay 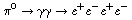 , one can measure the correlation of the
photon polarizations and determine the parity of the
, one can measure the correlation of the
photon polarizations and determine the parity of the