PROBLEM SET 3
Due Friday, February 12, 1999
Reading: Jackson, Secs. 12.3-12.11
Problems: Jackson, 12.5, 12.10, 12.11, 12.18;
LD 6
Addition to 12.11(c): The Stanford Linear Collider (SLC) can accelerate
polarized electrons and positrons. The particles collide
at the end of two semicircular arcs with radius 0.46 km. The energy of each
particle is 45 GeV when the SLC operates at the energy of the Z boson.
Suppose that the particles were longitudinally polarized when they entered
the arcs. How may times would the particle spins have rotated at the collision point? How would this be a problem if you wanted high longitudinal polarization
in the collision?
 |
|
12.5: This problem illustrates the use of the invariants
of the electromagnetic
field to simplify the calculation of particle motion in perpendicular
E and B fields. However, the simple results are not in the
original Lorentz frame. Explain carefully how the results in the
original frame are to be obtained. A kinematic diagram may be useful.
You do not need to obtain explicit expressions for the motion in the
original frame.
12.10: How is this problem related to the earth's Van Allen
belt? To the aurora? For reference, the equatorial radii of the inner
and outer Van Allen belts are roughly 1.6 and 3.7 earth radii. The zone
of maximum auroral activity is centered at lattitude 68°.
12.11: Watch your units!
Recall that we are using Gaussian cgs units. See
the Appendix on units in Jackson, especially the tables. For reference,
e = 4.8 × 10-10 esu, c = 3 × 1010 cm/s,
1 eV = 1.9 × 10-12 erg.
|
 |
|
Hint for 12.18: Suppose that 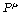 and and
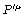 are defined by integrals of are defined by integrals of
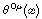 and and 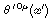 on the spacelike surfaces t = constant and t' = constant, respectively, where
the
on the spacelike surfaces t = constant and t' = constant, respectively, where
the 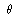 's
are connected by a Lorentz transformation with transformation matrix 's
are connected by a Lorentz transformation with transformation matrix
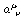 . Show that you can express . Show that you can express
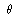 ' in terms of ' in terms of 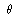 and change to the new surface to obtain the integral for
and change to the new surface to obtain the integral for
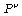 . .
|

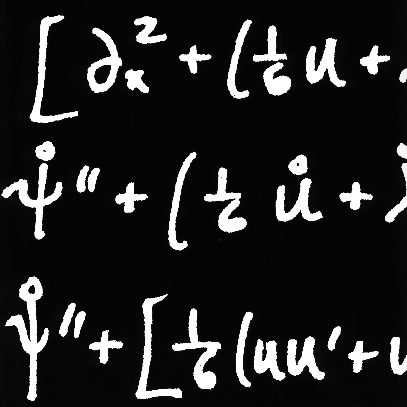 |
|
LD 7: Once you find E as a function of position in
the wire from the Lorentz force equation, it is simple to obtain the
charge density using Gauss' law, 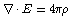 . .
|
Send comments or questions to:
ldurand@theory2.physics.wisc.edu
FURTHER OPTIONS:
© 1997, 1998, 1999 Loyal Durand
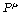 and
and
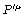 are defined by integrals of
are defined by integrals of
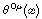 and
and 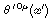 on the spacelike surfaces t = constant and t' = constant, respectively, where
the
on the spacelike surfaces t = constant and t' = constant, respectively, where
the 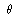 's
are connected by a Lorentz transformation with transformation matrix
's
are connected by a Lorentz transformation with transformation matrix
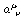 . Show that you can express
. Show that you can express
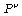 .
.

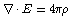 .
.