PROBLEM SET 5
Due Friday, March 5, 1999
Reading: Jackson, Secs. 14.1-14.5
Problems: Jackson, 13.12(a), 14.4, 14.9 plus addition,
14.12; LD9
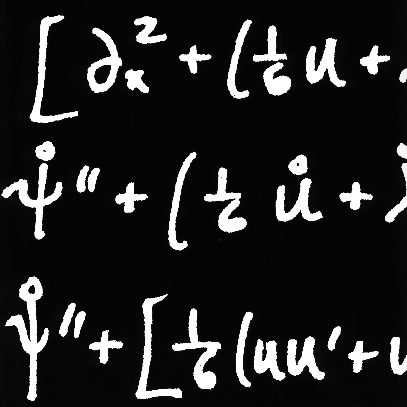 |
|
13.12(a): It is simplest to calculate using
the two-dimensional Fourier representation for the E
field in vacuum (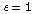 ) as input, and
evaluating the Fourier integrals directly. It is not necessary to use the
expressions in terms of Bessel functions. You will have to do some algebra
after you get the result for E in its initial "natural" form
to get the simplified form given by Jackson in the atatement of the problem.
A reference you might
find useful for general background is "Transition radiation from
ultrarelativistic particles", L. Durand, Phys. Rev. D 11, 89 (1975),
especially sections A and E. ) as input, and
evaluating the Fourier integrals directly. It is not necessary to use the
expressions in terms of Bessel functions. You will have to do some algebra
after you get the result for E in its initial "natural" form
to get the simplified form given by Jackson in the atatement of the problem.
A reference you might
find useful for general background is "Transition radiation from
ultrarelativistic particles", L. Durand, Phys. Rev. D 11, 89 (1975),
especially sections A and E.
|
|
|
14.4 and 14.12: Use vector algebra to
simplify the expressions for 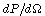 before
introducing explicit
forms for before
introducing explicit
forms for 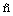 , , 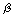 ,
and ,
and 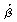 .
Question: why do the results for P in 14.4(a) and 14.4(b) differ by
exactly a factor of 2 for R=a? .
Question: why do the results for P in 14.4(a) and 14.4(b) differ by
exactly a factor of 2 for R=a?
|
 |
|
14.12: Treat the particle as relativistic as implied by the formulas
given. Expand the result in (b) for 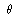 << 1
and for << 1
and for 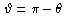 << 1
assuming that << 1
assuming that 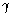 >> 1. Note you cannot simply set >> 1. Note you cannot simply set
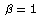 at the beginning and get sensible results,
so keep the first term in the expansion of at the beginning and get sensible results,
so keep the first term in the expansion of 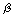 in powers of
in powers of 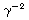 where necessary.
In what ranges of angle are the expansions valid? Explain. where necessary.
In what ranges of angle are the expansions valid? Explain.
|
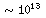 eV
moving in magnetic fields of ~1 mG. Use your result on the radiative
lifetime to estimate the time in years that it takes 10 GeV and 1 TeV
electrons in the Crab to lose one-half of their energy. Watch your units!
The Crab emits
eV
moving in magnetic fields of ~1 mG. Use your result on the radiative
lifetime to estimate the time in years that it takes 10 GeV and 1 TeV
electrons in the Crab to lose one-half of their energy. Watch your units!
The Crab emits 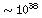 ergs/s in radiation.
For comparison, the
radiative output of the sun is
ergs/s in radiation.
For comparison, the
radiative output of the sun is 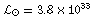 ergs/s.
There has been no change in the spectrum
of synchrotron radiation emitted by the ultrarelativistic electrons in
the nebula over the course of the last 30 years of active observations.
What constraints do these observations put on theories of the excitation
of the Crab?
ergs/s.
There has been no change in the spectrum
of synchrotron radiation emitted by the ultrarelativistic electrons in
the nebula over the course of the last 30 years of active observations.
What constraints do these observations put on theories of the excitation
of the Crab?
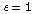 ) as input, and
evaluating the Fourier integrals directly. It is not necessary to use the
expressions in terms of Bessel functions. You will have to do some algebra
after you get the result for E in its initial "natural" form
to get the simplified form given by Jackson in the atatement of the problem.
A reference you might
find useful for general background is "Transition radiation from
ultrarelativistic particles", L. Durand, Phys. Rev. D 11, 89 (1975),
especially sections A and E.
) as input, and
evaluating the Fourier integrals directly. It is not necessary to use the
expressions in terms of Bessel functions. You will have to do some algebra
after you get the result for E in its initial "natural" form
to get the simplified form given by Jackson in the atatement of the problem.
A reference you might
find useful for general background is "Transition radiation from
ultrarelativistic particles", L. Durand, Phys. Rev. D 11, 89 (1975),
especially sections A and E.
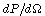 before
introducing explicit
forms for
before
introducing explicit
forms for 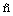 ,
, 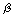 ,
and
,
and 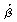 .
Question: why do the results for P in 14.4(a) and 14.4(b) differ by
exactly a factor of 2 for R=a?
.
Question: why do the results for P in 14.4(a) and 14.4(b) differ by
exactly a factor of 2 for R=a?
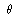 << 1
and for
<< 1
and for 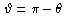 << 1
assuming that
<< 1
assuming that 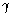 >> 1. Note you cannot simply set
>> 1. Note you cannot simply set
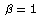 at the beginning and get sensible results,
so keep the first term in the expansion of
at the beginning and get sensible results,
so keep the first term in the expansion of 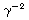 where necessary.
In what ranges of angle are the expansions valid? Explain.
where necessary.
In what ranges of angle are the expansions valid? Explain.