
| LD 12: Start with the case of a finite number of coupled
pendula, and describe carefully how you take the continuum limit.
The sine-Gordon equation appears in many other applications including such apparently different systems as Josephson-junction transmission lines, the propagation of spin waves in ferromagnetic lattices, the propagation of laser pulses in two-state materials, and models in quantum field theory. The topological properties of the equation and the associated boundary conditions lead to the existence of stable, finite-energy propagating solutions on a long rod despite the nonlinearity and dispersion in the waves. |

LD 13a It is helpful in handling the spatial integrations needed
to get rid of derivative operators acting on 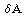 to write the remaining factors in the integrand in terms of B and
to write the remaining factors in the integrand in terms of B and
 , with the cross product expressed in terms
of , with the cross product expressed in terms
of 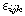 . You may assume that A and . You may assume that A and
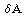 vanish at spatial infinity. vanish at spatial infinity.
LD 13b: Note that you cannot do a partial integration on t in calculating the Lagrangian L. However, you can show easily that the addition of a total time derivative to L does not change equations of motion. |

| LD 14a: Show explicitly, with appropriate arguments, how you
derive the equation of motion and boundary condition from the given
Lagrangian density.
LD 14b: The relation for 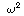 given
by the linearized Boussinesq equation includes the first-order correction
for wave dispersion properly, and is nonsingular in the limit of
short wave lengths in contrast to other approximations.
The nonlinear Boussinesq equation also includes the leading nonlinearity in the wave amplitude, but the correction is small for
small-amplitude waves. The equations apply to other than water waves, for
example, to waves in nonlinear lattices in an appropriate approximation.
See G.B. Whitham, Linear and Nonlinear Waves,
a classic, for a derivation of this equation and other approximate equations
for water waves. given
by the linearized Boussinesq equation includes the first-order correction
for wave dispersion properly, and is nonsingular in the limit of
short wave lengths in contrast to other approximations.
The nonlinear Boussinesq equation also includes the leading nonlinearity in the wave amplitude, but the correction is small for
small-amplitude waves. The equations apply to other than water waves, for
example, to waves in nonlinear lattices in an appropriate approximation.
See G.B. Whitham, Linear and Nonlinear Waves,
a classic, for a derivation of this equation and other approximate equations
for water waves.
|
Send comments or questions to: ldurand@theory2.physics.wisc.edu
FURTHER OPTIONS:
- WHAT'S NEW
- COURSE INFORMATION
- SYLLABUS
- HOMEWORK ASSIGNMENTS
- EXAMS
- WISCONSIN THEORY HOME PAGE
© 1997, 1998, 1999 Loyal Durand