
PROBLEM SET 9
Due Friday, April 9, 1998
Problems: LD 15, 16, 17

| LD 15a: Show in detail how you obtain the equation of motion
and the boundary conditions. The equation of motion can be written
simply at the end in terms of the Laplacian, a form that shows the
underlying symmetry of the problem.
b: After the time dependence is separated out using a Fourier representation, the equation of motion becomes a fourth order differential equation in the two spatial variables. It must have sixteen independent solutions before the boundary conditions and other constraints are imposed. However, the behavior in the x and y directions is connected by the mixed term in the equation of motion. The boundary conditions also impose constraints on the x or y dependence for y or x fixed. As a result, the solutions with the boundary conditions imposed cannot be written in the familiar form of a function of x multiplied by a function of y. Show for this problem that the only single-frequency modes symmetrical under a change in the sign of x or y are of the "bending beam" type, and combine those modes to obtain the modes with a fixed origin (Chladni plate). |

| LD 16: You do not need to derive the lagrangian densities for bending and compression from the beginning, but give your reasoning. Note that there is only one free boundary for the motion in z. |

Comment: If 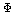 is treated as a
canonical variable for the electromagnetic field with charges and
currents present, the fact that there is no time derivative of is treated as a
canonical variable for the electromagnetic field with charges and
currents present, the fact that there is no time derivative of
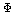 in the Lagrangian density implies that the
canonical momentum in the Lagrangian density implies that the
canonical momentum 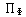 conjugate to conjugate to
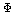 vanishes identically, a result inconsistent
with a nonzero Poisson bracket between these variables The vanishing of vanishes identically, a result inconsistent
with a nonzero Poisson bracket between these variables The vanishing of
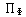 is an example of what
is called a "second class constraint" by Dirac, who developed the
Hamiltonian approach for constrained systems. The constraint can be
applied to the solutions of the equations
of motion, but not within the canonical formalism.
See Sudarshan and Mukunda, Classical Dynamics, for a
discussion of constrained Hamiltonian systems and the Dirac bracket
formalism. The hidden Lagrangian or Hamiltonian constraints on the
electromagnetic field make this most familiar example of a field theory
unexpectedly subtle. is an example of what
is called a "second class constraint" by Dirac, who developed the
Hamiltonian approach for constrained systems. The constraint can be
applied to the solutions of the equations
of motion, but not within the canonical formalism.
See Sudarshan and Mukunda, Classical Dynamics, for a
discussion of constrained Hamiltonian systems and the Dirac bracket
formalism. The hidden Lagrangian or Hamiltonian constraints on the
electromagnetic field make this most familiar example of a field theory
unexpectedly subtle.
|
Send comments or questions to: ldurand@theory2.physics.wisc.edu
© 1997, 1998, 1999, Loyal Durand